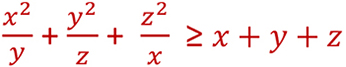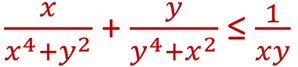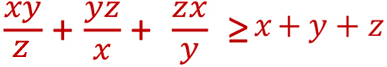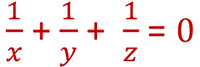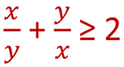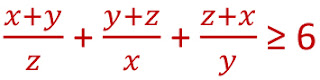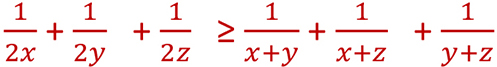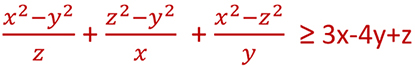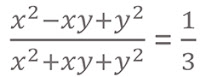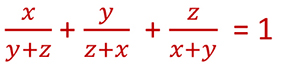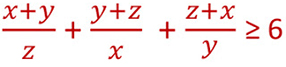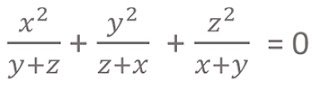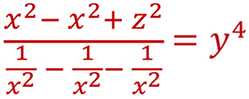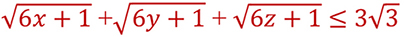Solutions du Olympiade Math Algèbre Niveaux 01

Exercice 01

x,y,z trois nombres réels strictement positifs m

Montrer que :

Solution

Exercice 02

x,y deux nombres réels strictement positifs

Montrer que :

Solution

Exercice 03

x,y deux nombres réels tel que:
x + y = 1
montrez que :

xy ≤ 1/4

Solution

Exercice 04

x,y,z trois nombres réels positifs

tel que : 2(z²-y²) = 3x²
Trouvez le plus grande de ces trois nombres

Solution

Exercice 05

x,y,z trois nombres réels strictement positifs

Montrer que :

(x+y)(y+z)(z+x) ≥ 8 xyz

Solution

Exercice 06

x,y,z trois nombres réels strictement positifs

Montrer que:

Solution

Exercice 07

x,y,z trois nombres réels non nul

tel que: (x+y+z)² = x²+y²+z²
Montrer que :

Solution

Exercice 08

x,y,z trois nombres réels strictement positifs.

Montrer que:

Solution

Exercice 09

x,y,z trois nombres réels strictement positifs

1- Montrer que :

2- En déduire que :

Solution

Exercice 10

x,y,z trois nombres réels strictement positifs

et m ∊ IR; Tel que :
xyz = 1 &

Montrer que : m = 1/2.

Solution

Exercice 11

x,y,z trois nombres réels strictement positifs
1- Montrer que :

2- En déduire que :

Solution

Exercice 12

x,y deux nombres réels strictement positifs

Montrer que :

Solution

Exercice 13

Soient x, y, z des nombres strictement positifs

Tel que : x≥y≥z

Montrer que :

Solution

Exercice 14

Pour quelle valeur de a l’équation:

|x-1|+|x-2|+|x-3|+|x-4|+|x-5| = a

admet – elle une solution unique ?

Solution

Exercice 15

on donne:

1³+2³+…..14³+15³=14400

Calculer

2³+4³+6³…..28³+30³

Solution

Exercice 16

on donne:

x= 1²-2²+3²-4²…..+99²-100²

y=1+2+3+4…….+99+100

Montrer que :

x+y=0

Solution

Exercice 17

x et y deux nombres réels non nul tel que:

calculer x / y

Solution

Exercice 18

x,y et z trois nombres réels tel que:

x+y+z≠0 &

Montrer que :

Solution

Exercice 19

x,y et z trois nombres réels non nuls,
Tel que:

Montrer que:

(x+y+z)²=x²+y²+z²

Solution

Exercice 20

x,y et z trois nombres réels strictement positifs,

montrer que:

Solution

Exercice 21

x nombre réel strictement positif,

tel que: x² +1/x² = 7

Calculer

Solution

Exercice 22

x,y et z trois nombres réels non nuls,

Tel que:

Montrer que :

Solution

Exercice 23

x,y deux nombres réels tel que:

Montrer que

x+y=0

Solution

Exercice 24

x nombre réal,
Tel que : x>1 et

Montrer que :

14x+1=x²

Solution

Exercice 25

x et y deux nombres différents strictement positifs

Tel que :

Calculer x/y

Solution

Exercice 26

x et y deux nombres différents

Tel que :

x²=y+2019 & y²=x+2019

Calculer xy

Solution

Exercice 27

Déterminer tous les couples (x, y) de nombres réels tels que :

|x + y| = 3 et xy = −10.

Solution

Exercice 28

x,y et z trois nombres réels strictement positifs,

Montrer que :

Solution

Exercice 29

x,y deux nombres réels
Tel que : x >1 et y>1

Montrer que :

Solution

Exercice 30

Calculer

Solution

Exercice 31

1- m nombre réel strictement positif

Montrer que:

m+1/m ≥ 2

2- x,y,z et t des nombres réels strictement positifs.

Montrer que:

Solution

Exercice 32

1- a,b,c trois nombres réels.

Montrer que :

(a+b+c)² ≤ 3(a²+b²+c²)

2- x,y,z des nombres réels strictement positifs.
Tel que : x+y+z=1.

Montrer que:

Solution

Exercice 33

Soient x et y deux nombres positifs.
Tels que:

Montrer que:

Solution

Exercice 34

Soient x et y deux nombres positifs.
Tels que:

Montrer que x = y = z.

Solution

Liens utiles :

L’Olympiade Internationale de Mathématiques (OIM)
site officiel de l’OIM, fondation de l’OIM

Olympiade de Maths, c’est une gymnastique de l’esprit, Ce qu’il faut c’est 4math.net et beaucoup de pratiques

4math.net Le première clé pour être bon en maths