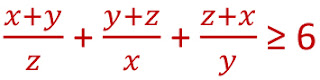Olympiade de Mathématiques( compétition de mathématiques destinée aux élèves des lycées et collèges)
▶️ Olympiade de Math – Algébre Niveaux 01 – Exercice 09
x,y,z trois nombres réels strictement positifs
Montrer que:
(frac{x+y}{z}+frac{y+z}{x}+frac{z+x}{y}≥6)
solution:
∸∸∸ ▶️ – 1- ◀️
on a (x-y)²≥ 0
⇾ x²+y²≥2xy & x,y≥0
⇾ x²/xy + y²/xy ≥2
▶️ x/y + y/x ≥2 ①
▶️ – 2- ◀️on poseA= (x+y) / z + (y+z) / x + (x+z) / y A= x/z + y/z + y/x + z/x + x/y + z/yA= (x/z +z/x) + (y/z + z/y)+ (y/x + x/y)① ⇾ y/x + x/y ≥2 ≡ y/z + z/y≥2 ≡ y/z + z/y≥2▶️ (x+y) / z + (y+z) / x + (x+z) / y ≥ 6
Liens utiles :
L’Olympiade Internationale de Mathématiques (OIM)
site officiel de l’OIM, fondation de l’OIM
Olympiade de Maths, c’est une gymnastique de l’esprit, Ce qu’il faut c’est 4math.net et beaucoup de pratiques
4math.net Le première clé pour être bon en maths