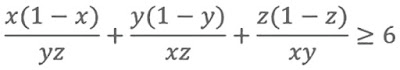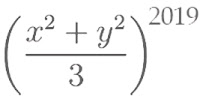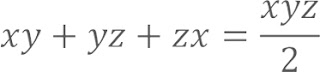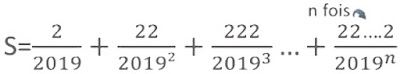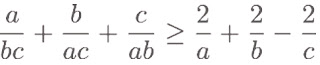Olympiade de Mathématique
( compétition de math destinée aux élèves des lycées et collèges)
Des exercices et sujets corrigés pour s’entraîner.
♦️ Exercice 01
a, b, c, d quatre nombres réels tel que :
a + b + c + d = 4
Montrer que
ab + bc + cd + da ≤ 4.
♦️ Exercice 02
x,y,z trois nombres réels strictement positifs
tel que x<y+z
Montrer que:
♦️ Exercice 03
x,y,z trois nombres réels positifs deux à deux distincts positifs et différents de zéro.
Tel que:
Montrer que: xyz = 1
♦️ Exercice 04
Ta,b et c trois longueur d’un triangle
Montrer que:
(a + c – b )² < 4 a c
♦️ Exercice 05
Soit a un nombre réel.
Combien de solutions le système suivant a-t-il ?

♦️ Exercice 06
1- Soient a, b, c, d des nombres réels
Tels que: a ⩽ b et c ⩽ d.
Montrer que :
ac + bd ≥ ad + bc.
2- Soient x, y > 0.
Montrer que :
Montrer que :
x³/y + y³/x ≥ x²+y²
♦️ Exercice 07
Soient x, y, z trois nombres réels strictement positifs.Tel que:
x/x’ = y/y’ = z/z’
Montrer que:
x/x’ = y/y’ = z/z’
Montrer que:
♦️ Exercice 08
Soient x, y deux nombres réels non nuls.
tel que: (x-y)(3x-2y)=xy
tel que: (x-y)(3x-2y)=xy
Calculer: (x+y) / (x-y)
♦️ Exercice 09
x,y,z,w nombres réels strictement positifs.
tel que :
x/y = y/z = z/w
Montrer que :
x/y = y/z = z/w
Montrer que :
♦️ Exercice 10
x,y,z nombres réels strictement positifs.
tel que : x+y+z=3
♦️ Exercice 11
x,y nombres réels.
Tel que :
Tel que :
Montrer que : x²-y²+z²=1
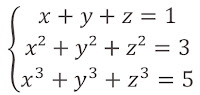
Calculer: x/y.
♦️ Exercice 30
♦️ Exercice 12
a, b et c trois nombres réels.
Montrer que :
a²+ 4b²+ 8c² ≥ 3ab + 4bc + 2ca.
♦️ Exercice 13
1- Montrer que:
si x² + y² = x + y = 1 alors xy = 0.
2- Montrer que:
si x³ + y³ + z³ = x² + y² + z² = x + y + z = 1
alors xyz = 0.
♦️ Exercice 14
x,y et z trois réels tel que:
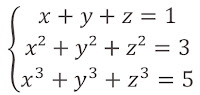
Montrer que: xyz=1/3.
♦️ Exercice 15
soit x un nombre réal non nul,
Tel que: x²-x+1=0
Calculer x²º²º + 1 / x²º²º ?
♦️ Exercice 16
soit x,y deux nombres réal , tel que:
Montrer que: x+y=0
♦️ Exercice 17
soit x,y,z x,y,z trois nombres réels, positif strictement positifs.
Tel que: x+y+z=1
♦️ Exercice 18
Calculer x ?
♦️ Exercice 19
Trouvez Tous les nombres x,y et z strictement positifs.Tel que: x+y+1/z = y+z+1/x = z+x+1/y =3
♦️ Exercice 20
1- Soient a,b,u et v de IR*+.
Montrer que:
a²/u + b²/v ≥ (a+b)² / (u+v)
a²/u + b²/v ≥ (a+b)² / (u+v)
Quand est-ce qu’on a l’égalité ?
2- Montrer que Pour tout x, y et z de IR*+ on a:
♦️ Exercice 21
Soient x et y deux nombres réels distincts.
Tels que: x+1=(y-1)² & y+1=(x-1)².
♦️ Exercice 22
Soient x et y deux réels stridulements positifs distincts. Tel que:
Calculer: x/y.
♦️ Exercice 23
Soient x et y deux réels positifs.
Montrer que:
♦️ Exercice 24
Soient x,y et z des nombres réels strictement positifs. Tel que:
Montrer que:

♦️ Exercice 25
Résoudre l’équation:
♦️ Exercice 26
♦️ Exercice 27
Soit a, b, c des nombres réels positifs.
Tel que: a≥3, b≥3 et c≥3.
Montrer que:
3(abc + b + 2c)≥2(ab + 2ac + 3bc).
♦️ Exercice 28
a,b,c des réels strictement positifs.
Tel que a+b+c=6.
Tel que a+b+c=6.
Montrer que:
(a+a/b)² + (b+b/c)²+ (c+c/a)² ≥ 27
♦️ Exercice 29
♦️ Exercice 30
Soit x un réel tel que » x + 1/x » est un entier.
Montrer que:
pour tout n ∊IN, » xⁿ + 1/xⁿ » est un entier.
Montrer que:
pour tout n ∊IN, » xⁿ + 1/xⁿ » est un entier.
voir solution
♦️ Exercice 31
Soit x,y,z des réels, Tel que:
x, y, z> 0 & x≤2 & y≤3 & x+y+z=11
Montrer que: xyz ≤36.
Liens utiles :
L’Olympiade Internationale de Mathématiques (OIM)
Olympiade de Maths, c’est une gymnastique de l’esprit, Ce qu’il faut c’est 4 math .net et beaucoup de pratiques.
4 math .net Le première clé pour être bon en maths
4 math .net Le première clé pour être bon en maths