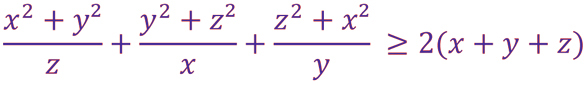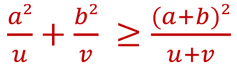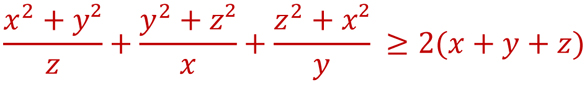Olympiade de Mathématique
( compétition de math destinée aux élèves des lycées et collèges)
Des exercices et sujets corrigés pour s’entraîner.
Olympiade Math – Algèbre 02 – Exercice 20
1- Soient a,b,u et v de IR*+.
Montrer que:
Quand est-ce qu’on a l’égalité ?
2- Montrer que Pour tout x, y et z de IR*+ on a:
Olympiade de Maths, c’est une gymnastique de l’esprit, Ce qu’il faut c’est 4math.net et beaucoup de pratiques
4math.net Le première clé pour être bon en maths
pour montrer que:
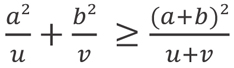
est équivalente à: (a²v+b²u)(u+v) ≥ uv(a+b)²
calculons la différence:
A= (a²v+b²u)(u+v)-uv(a+b)²
A= a²vu+a²v²+b²u²+b²uv-uva²-2abuv-uvb²
A= a²v²+b²u²-2abuv
A= (av-bu)² ≥ 0
Donc:
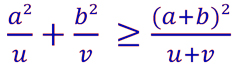
* L’égalité est vérifiée si :
A=0 ➝ av-bu=0
➨ av=bu.
2- Par application du résultat de la question précédente on prend:
a=z,b=y,u=y,v=z:
de même pour:
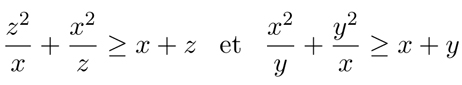
le résultat en découle facilement
(Somme terme par terme)
