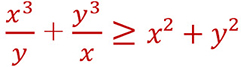Olympiade Math – Algèbre 02 – Ex 06

Olympiade de Mathématiques
( compétition de mathématiques destinée aux élèves des lycées et collèges)

▶️ Olympiade Math – Algèbre 02 – Exercice 06

1- Soient a, b, c, d des nombres réels 
tels que: a ⩽ b et c ⩽ d.
 Montrer que :

ac + bd ≥ ad + bc.
2- Soient x, y > 0. 
Montrer que :

Solution

1)- Calculons  la différence :
ac + bd – ad + bc=a(c-d)+b(d-c)
ac + bd – ad + bc=(d-c)(b-a)≥0

➨ ac + bd ≥ ad + bc.

2)- On a
* x²+y² ≥ 2xy (྾ x/y )
x³/y  + xy ≥ 2x² ①
*x²+y² ≥ 2xy (྾ y/x ) 
xy  + y³/x ≥ 2y² ②
①+② x³/y +y³/x+2xy ≥ 2x²+2y²
➝ x³/y +y³/x ≥ 2x²+2y²+2xy③
or 2x²+2y²+2xy=(x+y)²+x²+y²≥x²+y²
③ ➨ x³/y +y³/x ≥ x²+y²

Liens utiles : 
L’Olympiade Internationale de Mathématiques (OIM)
site officiel de l’OIM, fondation de l’OIM
Olympiade de Maths, c’est une gymnastique de l’esprit, Ce qu’il faut c’est 4math.net et beaucoup de pratiques
4math.net Le première clé pour être bon en maths