Exercice 1: (3 Pts)

Thème Analyse :

Partie A:
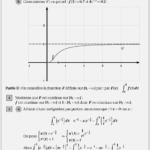
On considère la fonction \(f\) définie sur \([0,+∞[\) par :
si \(x>0 \): \(f(x)=(1+\frac{1}{x}) e^{-\frac{1}{x}}\)
f(0)=0
Soit la courbe de \(f\) dans un repère orthonormé \(( O; \vec{ i }, \vec{ j })\)
(unité graphique : \(2 cm\) )
1) Montrer que:
\(f\) est continue et dérivable à droite en \(0 .\)
2- a) Calculer \(\lim _{x➝+∞} f(x)\)
puis interpréter graphiquement le résultat obtenu.
b) Dresser le tableau de variation de \(f\).
3-a) Montrer que:
\(C\) admet un point d’inflexion que l’on précisera.
b) Construire \(C ;\)
en prend \(: f(1) \approx 0.7\) et \(4 e ^{-3} \approx 0.2\)

Partie B :
On considère la fonction \(F\) définie sur \([0,+∞[\) par:
\(F(x)=\int_{x}^{1} f(t) dt\)
1-1) Montrer que:
\(F\) est continue sur \(0 ,+∞[ \)
2-a) A l’aide d’une intégration par parties, montrer que ∀x>0:
\(\int_{x}^{1}(e^{-\frac{1}{t}}) dt=e^{-1}-x \cdot e^{-\frac{1}{x}}-\int_{x}^{1}(\frac{1}{t} e^{-\frac{1}{t}}) dt\)
b) Pour \(x>0 ;\) calculer :
\(\int_{x}^{1}(1+\frac{1}{t}) e ^{-\frac{1}{t}} d t\).
Puis montrer que:
\(\lim _{x ➝ 0^{+}}\int_{x}^{1} f(x) d x=\frac{1}{e}\).
3) On considère la suite \((u_{n})\) définie sur \(N\) par:
\(u_{n}=F(n)-F(n+2)\)
a) En utilisant le théorème des accroissements finis,
montrer que :
\((∀n∈ N )(∃ v_{n}∈] n, n+2[), u_{n}=2(1+\frac{1}{v_{n}}) e ^{-\frac{1}{v_{n}}}\)
b) Montrer que \(∀n∈IN ^{*} \):
\(2(1+\frac{1}{n}) e ^{-\frac{1}{n}}<u_{n}<2(1+\frac{1}{n+2}) e ^{-\frac{1}{n+2}}\).
En déduire \(\lim _{n ➝+∞} u_{n}\).

Partie C:
1-a) Montrer que:
\((∀n∈IN ^{*})(∃! α_{n}>0), f(α_{n})= e ^{-\frac{1}{n}}\)
b) Montrer que la suite \((α_{n})\) est croissante.
c) Justifier que \(∀n∈IN ^{*} \) on a :
\(-\frac{1}{α_{n}}+\ln (1+\frac{1}{α_{n}})=-\frac{1}{n}\)
2-a) Montrer que \(∀ t \geq 0,1-t≤ \frac{1}{1+t}≤ 1-t+t^{2}\)
b) En déduire que:
\((∀x \geq 0),-\frac{x^{2}}{2}≤ -x+\ln (1+x)≤ -\frac{x^{2}}{2}+\frac{x^{3}}{3}\)
3) Soit \(n\) un entier tel que \(n \geq 4\)
a) Vérifier que \(α_{4} \geq 1\)
puis déduire que \(α_{n} \geq 1\)
sachant que \(e ^{\frac{3}{4}} \geq 2\)
b) Montrer que :
\(1-\frac{2}{3 α_{n}}≤ \frac{2 α_{n}^{2}}{n}≤ 1 .\)
(On peut utiliser : (1-c) et (2-b) partie C:
c) Montrer que : \(\sqrt{\frac{n}{6}}≤ α_{n} .\)
En déduire \(\lim _{n ➝+∞} α_{n}\)
d) Calculer:
\(\lim _{n ➝+∞}(α_{n} \sqrt{\frac{2}{n}})\)

Exercice 2: (3 Pts)

Thème Arithmétiques:

Les parties A et B sont indépendantes

Partie A :
Afin de crypter un message, on utilise un chiffrement affine Chaque lettre de l’alphabet est associée à un nombre entier comme indiqué dans le tableau ci-dessous:

Soit \(x\) le nombre associé à la lettre à coder.
On détermine le reste \(y\) de la division euclidienne de \(7 x+5\) par 26 ,
puis on en déduit la lettre associée à \(y\)
(c’est elle qui code la lettre d’origine).
Exemple : M correspond à \(x=12 .\)
On a \(7×12+5=89\)
Or \(89 ≡ 11[26]\) et 11 correspond à la lettre \(L_{2}\)
donc la lettre M est codée par la lettre L.
1) Coder la lettre L.
2-a) Soit \(k\) un entier relatif.
Montrer que si \(k ≡ 7 x[26]\) alors \(15 k ≡ x[26]\).
b) Démontrer la réciproque de l’implication précédente.
c) En déduire que \(y ≡ 7 x+5\) [26] équivaut à \(x ≡ 15 y+3[26]\).
3) À l’aide de la question précédente décoder la lettre \(F\).

Partie B :
On considère les suites \((a_{n})\) et \((b_{n})\) telles que:
\(a_{0}\) et \(b_{0}\) sont des entiers compris entre 0 et 25 inclus
et pour tout entier naturel:
\(n, a_{n+1}=7 a_{n}+5\) et \(b_{n+1}=15 b_{n}+3\).
Montrer que pour tout entier naturel \(n\):
\(a _{n}=(a_{0}+\frac{5}{6})×7^{n}-\frac{5}{6}\).
On admet pour la suite du problème que:
\((∀n∈ N ), b_{n}=(b_{0}+\frac{3}{14})×15^{n}-\frac{3}{14}\).

Exercice 3: (3 Pts)

Thème Nombres complexes:

On considère les nombres complexes \(z_{n}\) définis, pour tout entier naturel \(n\), par:
\(z_{0}=1\) et \(z_{n+1}=(1+ i \frac{\sqrt{3}}{3}) z_{n}\)
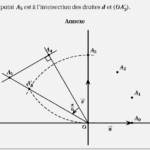
On note \(A_{n}\) le point d’affixe \(z_{n}\) dans le repère orthonormé
\(( O ; \vec{ u }, \vec{ v })\) de l’annexe.
L’objet de cet exercice est d’étudier la construction des points \(A_{n}\)
1-a) Vérifier que:
\(1+ i \frac{\sqrt{3}}{3}=\frac{2}{\sqrt{3}} e ^{ i \frac{\pi}{6}}\).
b) En déduire:
\(z_{1}\) et \(z_{2}\) sous forme exponentielle.
2-a) Montrer que pour tout entier naturel n:
\(z_{n}=(\frac{2}{\sqrt{3}})^{n} e ^{ i n \frac{\pi}{6}}\).
b) Pour quelles valeurs de \(n\), les points \(O , A_{0}\) et \(A_{n}\) sont-ils alignés?

3) Pour tout entier naturel \(n\), on pose \(d _{ n }=|z_{n+1}-z_{n}|\).
a) Interpréter géométriquement \(d_{n}\).
b) Calculer \(d_{0}\).
c) Montrer que ∀n∈ IN ^{*}:
\(z_{n+2}-z_{n+1}=(1+ i \frac{\sqrt{3}}{3})(z_{n+1}-z_{n})\).
d) En déduire que la suite \((d_{n})_{n \geqslant 0}\) est géométrique
puis que ∀n∈ IN : \(d_{n}=\frac{\sqrt{3}}{3}(\frac{2}{\sqrt{3}})^{n}\)
4-a) Montrer que pour tout entier naturel n:
\(|z_{n+1}|^{2}=|z_{n}|^{2}+d_{n}^{2}\).
b) En déduire que pour tout entier naturel n:
le triangle \(OA_{n}A_{n+1}\) est rectangle en \(A_{n}\).
c) Construire, à la règle non graduée et au compas, le point \(A_{5}\)
sur la figure de l’annexe.
d) Justifier cette construction.