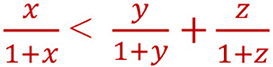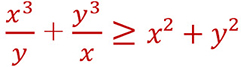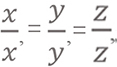Solutions du Olympiade Math Algèbre Niveaux 02

  Olympiade Math – Algèbre 02 – Exercice 01 

a, b, c, d quatre nombres réels tel que :

a + b + c + d = 4

Montrer que 
ab + bc + cd + da ≤ 4.
  Olympiade Math – Algèbre 02 – Exercice 02 

x,y,z trois nombres réels strictement positifs 

tel que : x<y+z

Montrer que 

  Olympiade Math – Algèbre 02 – Exercice 03 

x,y,z trois nombres réels positifs deux à deux distincts positifs et différents de zéro tel que:

Montrer que:
xyz = 1

  Olympiade Math – Algèbre 02 – Exercice 04 
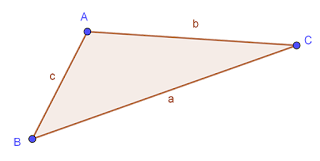
a,b et c trois longueur d’un triangle 
Montrer que:
(a + c – b ) ² < 4 a c


  Olympiade Math – Algèbre 02 – Exercice 05 

Soit a un nombre réel.
Combien de solutions le système suivant a-t-il ?

  Olympiade Math – Algèbre 02 – Exercice 06 

1- Soient a, b, c, d des nombres réels tels que:
 a ⩽ b et c ⩽ d.
Montrer que:

ac + bd ≥ ad + bc.

2- Soient x, y > 0. 
Montrer que:

  Olympiade Math – Algèbre 02 – Exercice 07 

Soient x, y, z trois nombres réels strictement positifs. tel que: 

Montrer que:

  Olympiade Math – Algèbre 02 – Exercice 08 

Soient x, y deux nombres réels non nuls.
tel que: (x-y)(3x-2y)=xy
 calculer

Liens utiles : 
L’Olympiade Internationale de Mathématiques (OIM)
site officiel de l’OIM, fondation de l’OIM
Olympiade de Maths, c’est une gymnastique de l’esprit, Ce qu’il faut c’est 4math.net et beaucoup de pratiques

4math.net Le première clé pour être bon en maths