Bac Economie et Gestion Session contrôle 2019
Pdf Avec Correction
Durée de l’épreuve 2h
L’épreuve est composée de trois exercices et un problème
indépendants entre eux et répartis suivant les domaines comme suit:
* Calcule Matriciel 1 (5 points )
* Calcule Matriciel 2 (5 points )
* Etude d’une fonction numérique (5 points )
* probabilité (5 points )
* Calcule Matriciel 1 (5 points )
On donne les matrices:
A=\(\left(\begin{array}{ccc}1 & 1 & 1 \\ 2 & 4 & 5 \\ 5 & 6 & 8\end{array}\right)\) et B=\(\left(\begin{array}{ccc}2 & -2 & 1 \\ 9 & 3 & -3 \\ -8 & -1 & 2\end{array}\right )\)
1) a) Calculer A×B.
b) En déduire la matrice inverse de A
2) Un atelier de couture confectionne 400 pantalons, en trois modèles \(P_{1}, P_{2}\) et \(P_{3}\) Il dispose d’un tissu de longueur 492 mètres (ayant une largeur fixe) pour la couture de ces pantalons avec un coút total de 5680 dinars. La longueur du tissu et le coût de couture d’un pantalon de chaque modèle sont donnés Dans le tableau suivant:
\(\begin{array}{|l|c|c|c|}\hline Type de pantalon & P _{1} & P _{2} & P _{3} \\\hline C.C.P & 8 & 16 & 20 \\\hline L.T & 1 & 1,2 & 1,6 \\\hline\end{array}\)
Avec:
C.C.P: Le coût de couture d’un pantalon (en dinars)
L.T: Longueur du tissu & (en mètres)
On se propose de déterminer le nombre de pantalons coudés de chaque modèle.
a) Montrer que la situation se traduit par le système
\[\left\{\begin{matrix} x+y+z=400\\2x+4 y+5 z=1420\\5x+6 y+8=2460\\ \end{matrix}\right.\]
b) Donner I’écriture matricielle de (S).
c) Déterminer alors le nombre de pantalons coudés de chaque modèle.
* Calcule Matriciel 2 (5 points )
On considère le graphe (Γ) Ci-contre
dont les sommets Sont \(A, B, C, D, E, F et G\)

1) Compléter le tableau suivant:
\(\begin{array}{|l|p{1in}|c|} \hline Sommet &A&B&C&D&E&F&G \\ \hline degré & & & & & & & \\ \hline \end{array}\)
b) Justifier que le graphe (Γ) admet une chaîne eulérienne.
c) Le graphe (Γ) admet-il un cycle eulérien ? Expliquer.
2) Donner la matrice M associée à ce graphe en respectant l’ordre alphabétique.
3) a) L’une des matrices suivantes P et Q est la matrice \(M^{3}\)
Indiquer laquelle en justifiant votre réponse:
\(P=\left(\begin{array}{rrrrrrr}6 & 9 & 9 & 11 & 4 & 6 & 6 \\ 9 & 8 & 12 & 12 & 4 & 7 & 11 \\ 9 & 12 & 8 & 12 & 4 & 11 & 7 \\ 11 & 12 & 12 & 12 & 4 & 12 & 12 \\ 4 & 4 & 4 & 4 & 2 & 6 & 6 \\ 6 & 7 & 11 & 12 & 6 & 6 & 10 \\ 6 & 11 & 7 & 12 & 6 & 10 & 6\end{array}\right)\)
\(et\; Q =\left(\begin{array}{rrrrrrr}2 & 9 & 9 & 11 & 4 & 6 & 6 \\ 9 & 8 & 12 & 12 & 4 & 7 & 11 \\ 9 & 12 & 8 & 12 & 4 & 11 & 7 \\ 11 & 12 & 12 & 12 & 4 & 12 & 12 \\ 4 & 4 & 4 & 4 & 2 & 6 & 6 \\ 6 & 7 & 11 & 12 & 6 & 6 & 10 \\ 6 & 11 & 7 & 12 & 6 & 10 & 6\end{array}\right)\)
b) Déterminer:
le nombre de chaines de longueur 3 joignant le sommet F au sommet G
* Etude d’une fonction numérique (5 points )
Soit \(f\) la fonction réelle définie sur IR par:
\(f(x)=e^{x}-e^{-x}+x\)
On désigne par (C) sa courbe représentative
dans un repère orthonormé \(( O,\vec{i},\vec{j})\)
1) Montrer que la fonction \(f\) est impaire.
2) a) Calculer \(\lim_{x➝+∞} f(x)\)
puis vérifier que: \(\lim_{x➝+∞}\frac{f(x)}{x}=+∞\)
et interpréter graphiquement ce résultat.
b) Justifier que \(f\) est dérivable sur IR
et que \(f ‘(x)>0\) pour tout réel x.
c) Dresser le tableau de variation de \(f\)
3) a) Montrer que O est un point d’inflexion pour la courbe (C).
b) Montrer que:
la tangente T à la courbe (C) au point O a pour équation y=3x.
4) a) Montrer que:
\(f\) réalise une bijective de IR sur IR.
(On notera dans la suite par \(f^{-1}\) la fonction réciproque de \(f\)
et on désignera par (C’) sa courbe représentative dans le repère orthonormé
\(( O,\vec{i},\vec{j})\)
b) Monter que:
\(f^{-1}\) est dérivable en 0, et déterminer (\(f^{-1}) ‘(0)\)
5) Tracer (T),(C) et (C’).
* probabilité (5 points )
Une petite entreprise commercialise des tapis et des lustres.
Un client quelconque se présente, il achète au plus un tapis et un lustre.
on probabilité pour que ce client achète un tapis est 0,2
– la probabilité pour que
ce client achète un lustre sachant qu’il a acheté un tapis est 0,7
– la probabilité pour que
ce client acheté un lustre sachant qu’il n’a pas acheté un tapis est 0,1
On note par:
T: ≪ l’événement le client achète un tapis≫
L: ≪ l’événement le client achète un lustre y.≫
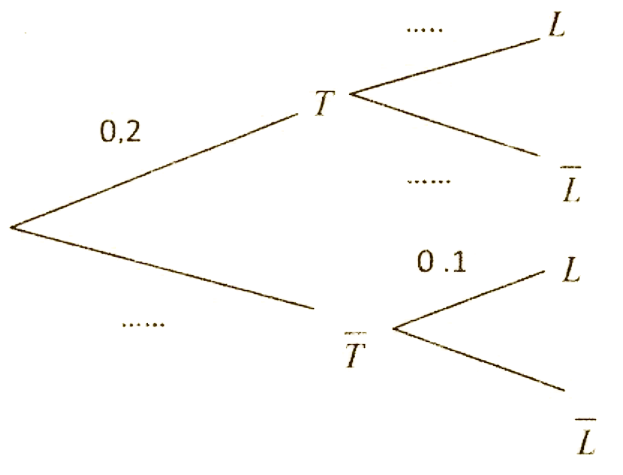 b) Calculer la probabilité de l’événement \(T \cap L\)
b) Calculer la probabilité de l’événement \(T \cap L\)
c) Montrer que la probabilité de l’événement L est égale à 0,22.
d) Calculer la probabilité pour que le client acheté un tapis ou un lustre.
2) Le prix d’un tapis est 150 dinars et celui d’un lustre est 50 dinars.
Soit X la variable aléatoire prenant pour valeur la dépense d’un client.
a) Recopier et compléter le tableau suivant:
\(\begin{array}{|l|p{1in}|c|} \hline x_{i}:\; Dépense (dinars)&0&50&150&200 \\ \hline p_{i}:\;& & & & \\ \hline \end{array}\)
donnant la loi de probabilité de X:
b) Calculer l’espérance mathématique de X
et donner une interprétation de la valeur ainsi trouvée.


