Olympiade de Mathématique
( compétition de math destinée aux élèves des lycées et collèges)
Des exercices et sujets corrigés pour s’entraîner.
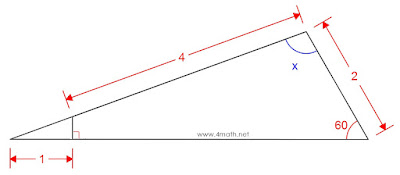
Soit la figure suivante:
Calculer x?
Soit H projection de A sur (BC)
* dans le triangle ABC:
Sin(α)=AH/AB & Sin(60)=AH/AC
Sin(α)xAB=Sin(60)xAC ①
* dans le triangle BEF:
Cos(α)=1/BE
BE=1/Cos(α)
AB=AE+BE
AB=4+1/Cos(α)
* calculons α
①⤵️
Sin(α)x(4+1/Cos(α))=2Sin(60)
4Sin(α)+tan(α)=Sin(60)/cos(α)
4Sin(α)=tan(60)-tan(α)
2Sin(α)xcos(α)=sin(60)xcos(α)-sin(α)xcos(60)
sin(2α)=sin(60-α)
2α=60-α
α=20
* dans le triangle ABC:
x+α+60=180
x=180-60-20
Donc: x=100
Olympiade de Maths, c’est une gymnastique de l’esprit, Ce qu’il faut c’est 4 math .net et beaucoup de pratiques. 4 math .net Le première clé pour être bon en maths