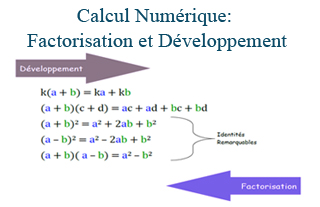
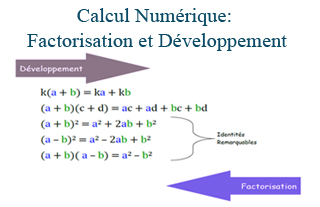
factorisation et développement
cours // exercices
Exercice 1:
Exercice 2:
E=x²-3x=x(x-3)
=(x+1)(3x-4+2x-3)
Exercice 3:
Exercice 4:
A=(5-3x)(x-2)-(15-9x)(3x+4)
=(5-3x)(x-2)-3(5-3x)(3x+4)
=(5-3x)((x-2)-3(3x+4))
=(5-3x)(x-2-9x-12)
=(5-3x)(-8x-14)
=(5-3x)-2(4x+7)
=-2(5-3x)(4x+7)
B=(3x-2)(5x+1)-(3x²-2x)-(21x-14)(6x-7)
=(3x-2)(5x+1-x+7(6x-7))
=(3x-2)(5x+1-x+42x-49)
=(3x-2)(46x-48)
=(3x-2)2(23x-24)
=2(3x-2)(23x-24)
Exercice 5:
développer:
A=(x+3)²= x²+6x+9
B=(2x-4)²= 4x²-16x+16
C=(10-11x)(10+11x =10² – (11x)² =100 – 121x²
Exercice 6:
factoriser:
A=x²(2x-1)+(4x²-1)
=x²(2x-1)+((2x)²-1²)
=x²(2x-1)+(2x-1)(2x+1)
=(2x-1)(x²+2x+1)
=(2x-1)(x+1)²
B=x²-14x+49
=x²-14x+7²
= (x-7)²
C=(x-3)(6x-7)-(x²-6x+9)
=(x-3)(6x-7)-(x-3)²
=(x-3)(6x-7-(x-3))
=(x-3)(6x-7-x+3)
=(x-3)(5x-4)
Exercice 7:
Résoudre les équations suivantes :
On a: 9x²-6x+1=0
Alors: (3x)²-6x+1²=0
Donc: (3x-1)² =0
C’est à dire: 3x-1=0
C’est à dire: 3x=1
Alors: x=1/3
D’ou la solution de cette équation est 1/3
On a: 25x²+40x+16=0
Alors: (5x)²+40x+4²=0
Donc: (5x+4)²=0
C’est à dire: 5x+4=0
C’est àdire: 5x=-4
C’est à dire: x=-4/5
D’ou la solution de cette équation est -4/5
On a: 4x²-25=0
Alors: (2x)²-5²=0
Donc: (2x-5)(2x+5)=0
C’est à dire: 2x-5=0 ou 2x+5=0
C’est à dire: 2x=5 ou 2x=-5
C’est à dire: x=5/2 ou x=-5/2
D’ou les solutions de cette sont 5/2 et -5/2
Exercice 8:
Résoudre les équations suivantes
On a: (2x+3)²-(1-4x)(2x+3)=0
Alors: (2x+3)(2x+3-1+4x)=0
Donc: (2x+3)(6x+2)
C’est à dire:(2x+3)2(3x+1)
C’est à dire:2(2x+3)(3x+1)
Donc: 2x+3=0 ou 3x+1=0
Alors: 2x=-3 ou 3x=-1
C’est à dire: x=-3/2 ou x=-1/2
D’ou les solutions de cette équation sont -3/2 et -1/2
On a: x²-4+(2x+4)(3x-5)=3(x+2)²
Alors: (x-2)(x+2)+(2x+4)(3x-5)-3(x+2)²=0
Donc: (x+2)(x-2+2(3x-5)-3(x+2))=0
C’est à dire: (x+2)(x-2+6x-10-3x-6)=0
C’est à dire: (x+2)(4x-18)=0
C’est à dire: (x+2)2(2x-9)=0
C’est à dire: 2(x+2)(2x-9)=0
Donc: x+2=0 ou 2x-9=0
Alors: x=-2 ou 2x=9
C’est à dire: x=-2 ou x=9/2
D’ou les solutions de cette équation sont -2 et 9/2