Calcul Numérique: Factorisation et Développement

 1- développement:

Quand on transforme un produit en une somme algébrique, on dit que l’on développe.
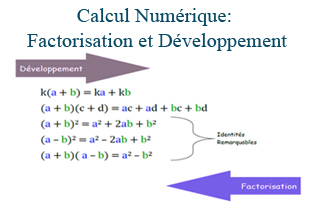
k;a et b désignent des nombres réels :
k(a+b) = ka+kb
k(a-b) = ka-kb

résultat:
a,b,c désignent des nombres réels:
(a+b)(c+d) = ac+ad+bc+bd

Exemple:
A=5(x-1)-(2x+3)(x-2)
=5x-5-(2x²-4x+3x-6)
=5x-5-2x²+4x-3x+6
=6x-2x²+1

Quand on transforme une somme algébrique en un produit , on dit que l’on factorise.
k,a et b désignent des nombres réels
ka + kb = k(a+b)
ka – kb = k(a-b)

Exemple:B=2x(x-1)-(x-1)(x+1)
=(x-1)(2x-(x+1))
=(x-1)(2x-x-1)
=(x-1)(x-1)

3- Identités remarquables : 

Pour tous nombres réels a et b:
(a+b)²=a²+2ab+b²
(a-b)²=a²-2ab+b²
(a-b)(a+b)=a²-b²

Exemple (1):développer : (2x+ 5)²
(2x+5)²=(2x)²+2☓2x☓5+5²
=4x²+20x+25

Exemple(2):

B=16x²+24x+9
= (4x)²+2☓4x☓3+3²
=(4x+3)²

-Équation du seconde degré résolue dans l’ordre des équations du premier degré par un inconnu:

Exemple:

x²+10x+25=0
x²+2*x*5+5²
(x+5)²=0
x+5=0
x=-5
D’où:
la solution de cette équation est -5

x²-2x+1=0
(x-1)²=0
x-1=0
x=1
D’où:
la solution de cette équation est 1

x²-9=0
x²-3²=0
(x-3)(x+3)=0
x-3=0 ou x+3=0
x=3 ou x=-3
D’où:
les solutions de cette équation sont :3 et -3

(2t-3)(t-2)-(t-2)²=0
(t-2)(2t-3-(t-2))=0
(t-2)(2t-3-t+2)=0
(t-2)(t-1)=0
t-2=0 ou t-1=0
t=2 ou t=1
D’où:
les solutions de cette équations sont 2 ou 1