Les Puissances 3ème collège Exercices

Entraînement

Exercice 1
Déterminer le signe de chacun des nombres suivants :
\((-4,0304)^{4} ;-(-\frac{5}{9})^{4} ; 314^{34} ;(-2016,2017)^{8} ; 27^{-9}\).

Exercice 2
Effectuer les calculs suivants:
A=\(\frac{6^{2}× 4^{2}}{10^{2}}\)
B=\(3^{3}-6× 4+8\)
C=\(2^{2}+3× 6+6^{2}-(4^{2}-6^{2})\)
D=\((4^{2}+6)^{-1}× 3×(3^{2}+1)\)

Exercice 3
Effectuer les calculs suivants:
A=\((-6)^{2}+2× 5+9:(-3)\)
B=\(-6^{2}+2×(5+9):(-3)\)
C=\(-6^{2}+(2× 5+9):(-3)\)
D=\(-(6^{2}+2)× 5+[9:(-3)]\)
E=\(-(6^{2}+2)×(5+9):(-3)]\)

Exercice 4
Effectuer les calculs suivants:
F=\(2-3× 4^{2}-(5-7)^{3}\)
G=\((2^{3}+4)^{-1}× 2×(3^{2}-1)\)
H=\(3^{2}-6× 2-7^{0}\)
I=\(2^{3}+3× 4+4^{2}-(2^{2}+5^{2})\)

Exercice 5
Simplifier :
J=\(6^{2}×(-6)^{5}× \frac{(-6)^{4}}{(-6)^{2}}×(6^{-2})^{-2}\)
K =\((\frac{5}{3})^{-2}×(\frac{-5}{3})^{-3}×(\frac{25}{9})^{-1}\)
L=\(2^{5}× 8^{15}× 1,25× 10^{-15}× 10^{170}\)

Exercice 6
a est un nombre réel négatif non nul.
Déterminer le signe de chacun des réels suivants:
\(a^{5}, a^{3}, a^{-4}, a^{-7},-a^{3} \text { et }(-a)^{9} \text {. }\)

Exercice 7
a est un nombre réel non nul.
Ecrire sous forme d’une seule puissance:
A=\(\frac{a^{6}× a^{-6}}{a^{-7}}\)
B=\(\frac{a^{-13}}{a^{-4}× a^{-7}}\)
C=\(\frac{a^{4}×(a^{-4})^{4}}{a^{-13}× a^{16}}\)
D=\(\frac{a^{-8}× a^{-12}}{(a^{-2})^{3}×(a× a^{-3})^{-1}}\)

Exercice 8
a et b sont deux nombres réels non nuls.
Simplifier:
Q=\((3 a )^{2}×(\frac{1}{3})^{3}×(\frac{ a }{3})^{-2}\)
R=\((\frac{3}{ a })^{3}×( ab )^{-3}×(\frac{1}{ a ^{-1}})^{-2}\)
S=\((3 a )^{3}×(\frac{1}{ a })^{2}×(\frac{ a }{3})^{4}\)
T=\((3 a )^{-2}×[(\frac{ a }{3})^{-2}]^{3}×[(2 a )^{2}]^{-1}\)

Exercice 9
\(a\) et \(b\) sont deux nombres réels non nuls.
Simplifier:
U=\([ a ^{3}×( a ^{-2})^{-1}]^{-2}×( a ^{-3}× a ^{4})^{2}\)
V=\(\frac{( a ^{-1}× b )^{-2}× a ^{2}× b ^{-4}}{( a ^{3}× b ^{2})^{-2}×( b ^{-3})^{-4}}\)
W=\(\frac{( ab )^{4}}{ a ^{-2} b ^{-1}}: \frac{( a ^{4} b ^{-3})^{-1}}{ a ^{2} b ^{-3}}\)
X=\(\frac{(2 a ^{-2} b ^{-3})^{-2}}{(3 a ^{3} b )^{2}}\)

Exercice 10
Calculer:
A=\((-\frac{1}{3})^{4}+(\frac{1}{3})^{-2}\)
B=\([1-(\frac{1}{3}+2^{-1})]^{-2}\)
C=\((\frac{1}{3})^{-3}+[(\frac{1}{2})^{-2}+(\frac{1}{3})^{-2}]^{-1}\)
D=\(3^{2}-(\frac{-2}{3})^{-2}+(-1)^{2019}×(\frac{5}{3})^{-3}\)

Exercice 11
Simplifier :
E=\([\frac{3^{6}×(24)^{-2}}{18^{3}×(2^{-3})}]^{-4}\)
F=\([\frac{((5^{7})^{2}× 3^{-4})^{-1}}{3^{-5}×(5^{2}× 3^{-1})^{-1}}]^{-2}\)
G=\([\frac{4^{-3}× 15^{-4}×(3^{-2})^{-1}}{(3^{-2})^{3}× 12^{4}× 5^{-4}}]^{4}\)

Exercice 12
\(0,007=7× 10^\ldots\)
\(20,16=2016× 10^\ldots\)
\(0,0002017=\ldots× 10^{-4}\)
\(195,7=\ldots× 10^{-2}\)

Approfondissement

Série 1

Exercice 1 :
a un nombre réel:
Ecrire chaque produit sous la forme \(a^{n}\) où \(n\) est un entier relatif
\(M=16× 2^{-3} ; N=81× 3^{6}\)
\(O=(10^{-3})^{-4}× 10000× 10^{5}× 0,001\)
\(P=135× 15× 45\)

Exercice 2:
Montrer que : \(64^{20}=32^{24} .\)
\(n\) est un nombre entier naturel impair.
Calculer \(E=2^{3}(-1)^{n+1}-(-3)^{2}(-1)^{n}\)

Exercice 3:
Déterminer l’entier relatif \(n\) dans chacun des cas suivants :
1) \(9^{2n}=3^{4}\)
2) \(2^{n+1}=\frac{1}{8}\)
3) \((\frac{1}{125})^{n}=5^{-2 n}× 125\)

Exercice 4 :
a est un nombre réel négatif non nul.
Déterminer le signe de chacun des réels suivants :
\(a^{5}, a^{8}, a^{-4}, a^{-7},-a^{3} \text { et }(-a)^{9}\)

Exercice 5:
Recopier et compléter chaque égalité :
\((3^{-6}) \cdots=3^{18}\)
\(a^{18}× a^{-3}=a^{-3}\)
\((\ldots a)^{3}=-27 a^{\cdots}\)
\(4^{-x}× 4^{-2}=1 ; \frac{a^{-8}}{a^{-m}}=a^{2}\)
\((\ldots )^{2}=169 a^{4}\)
\(\frac{2^{-4}× 2^{-\cdots}}{2^{5}}=2^{-7}\)
\((7^{7})^{-3}× 7^{\cdots }=7^{-14}\)

Exercice 6:
a et b sont deux nombres réels non nuls.
On donne:
\(E=\frac{(a^{2} b^{-1})^{-2}×(a^{-3} b^{2})^{-3}× a^{4}}{(a×(b^{2})^{-2})^{-1}×(a^{2} b)^{3}}\)
1) Simplifier E.
2) Calculer E lorsque : \(a=10^{3}\) et \(b=0,0001\)

Exercice 7:
a est un nombre réel non nul.
Ecrire sous forme d’une seule puissance:
\(A=\frac{a^{6}× a^{-8}}{a^{-7}}\)
\(B=\frac{a^{-13}}{a^{-4}× a^{-7}}\)
\(C=\frac{a^{4}×(a^{-4})^{4}}{a^{-13}× a^{16}}\)
\(D=\frac{a^{-8}× a^{-12}}{(a^{-2})^{3}×(a× a^{-3})^{-1}}\)

Exercice 8 :
a et b sont deux nombres réels non nuls.
Simplifier:
Q=\((3 a)^{2}×(\frac{1}{3})^{3}×(\frac{a}{3})^{-2}\)
R=\((\frac{3}{a})^{3}×(a (b)^{-3}×(\frac{1}{a^{-1}})^{-2}\)
S=\((3 a)^{3}×(\frac{1}{a})^{2}×(\frac{a}{3})^{4}\)
T=\((3 a)^{-2}×[(\frac{a}{3})^{-2}]^{3}×[(2 a)^{2}]^{-1}\)

Exercice 9:
a et b sont deux nombres réels non nuls. Simplifier:
\(u=[a^{3}×(a^{-2})^{-1}]^{-2}×(a^{-3}× a^{4})^{2} ; v=\frac{(a^{-1}× b)^{-2}× a^{2}× b^{-4}}{(a^{3}× b^{2})^{-2}×(b^{-3})^{-4}}\)
\(w=\frac{(a b)^{4}}{a^{-2} b^{-1}}: \frac{(a^{4} b^{-3})^{-1}}{a^{2} b^{-3}} ; \) \(x=\frac{(2 a^{-2} b^{-3})^{-2}}{(3 a^{3} b)^{2}}\)

Exercice 10:
Sachant que:
\(a^{3}=13824\) et \(a^{5}=7962624\)
1) Déterminer \(a^{2}\) et \(a^{6}\) sans calculer \(a\).
2) En déduire a .

Exercice 11:
Calculer:
a=\((\frac{9}{4})^{2018}×(\frac{16}{36})^{2018}\)
b=\([(\frac{5}{3})^{2}+(\frac{3}{7})^{-2}]^{-1}\)
Montrer que :
\([\frac{(3 \sqrt{5})^{2}}{135}]^{-2}=9\)

Série 2

Exercice 12:
Calculer :
a=\((2^{-2}+\frac{3}{4})^{100}\)
b=\(2^{-2}×(2,5)^{5}× 5^{-3}× 4^{5}\)
c=\(\frac{7^{-n+1}× 7^{n}}{7^{3 n}}×(343)^{n}\)

Exercice 13:
On donne: \( E=\frac{(a^{3} b^{-3})^{4}}{[(a^{-2})^{-5} b^{3}]^{-2}}\)
a – Montrer que : \(E=\frac{a^{32}}{b^{6}}\).
b. Calculer E lorsque :
\(a=3× 10^{-2}\) et \(b=27× 10^{3}\)
c. Donner l’écriture scientifique de \(E\).

Exercice 14:
1) Calculer:
\(a=\frac{1-(\frac{3}{4})^{-2}}{(\frac{\sqrt{7}}{3})^{2}}\)
2) b et c sont deux nombres réels tels que :
\(b=38,2× 10^{4}\) et \(a=0,003× 10^{8}\)
Donner l’écriture scientifique de \(b+c\).

Exercice 15:
1) Calculer \(x=(\frac{3}{5})^{-3}×(\frac{2}{5})^{2}× \frac{2^{-7}}{5^{-2}}\)
2) On pose : \(\alpha=\frac{4× 300^{2}×(10^{-4})^{-2}}{(0,01)^{-3}}\)
\(a-\) Montrer que \(\alpha=36× 10^{6}\)
b. Déterminer l’écriture scientifique de \(\alpha\).
3) Montrer \(28× 6^{n}-6^{n+1}\) est un multiple de 11 . (ou n est un entier naturel)

Exercice 16:
Déterminer l’entier naturel \(n\) tel que :
\(7(3^{n}+3^{n+1}+3^{n+2})=21^{n}×13\)
\(15^{3 n+5}=3^{2 n+6}× 5^{4 n+4}\)

Exercice 17:
\(a\) et \(b\) sont deux nombres réels positifs non nuls
\(m\) et \(n\). un entier naturel non nul. Simplifier \(E\) et \(F\) :
E=\((\frac{b}{a})^{-n}× b^{n+1}× a^{-n}\)
F=\(\frac{b^{n+1}+b a}{b^{n}+a}\)

Exercice 18:
\(a\) et \(b\) sont deux nombres réels non nuls.
\(m\) et \(n\) sont deux entiers relatifs.
Simplifier R et S :
R=\(\frac{a^{n}× b^{m+n}+a^{m+n}× b^{n}}{a× b^{m+1}+a^{m+1} b}\)
S=\(\frac{4 a^{n}+4}{2 a^{n}+2+4 a^{n}}\)

Exercice 19:
Soit a et b deux nombres réels non nuls.
On considère le nombre :
A=\(\frac{a^{-2} b(a^{2} b^{-1})^{4} a^{-3} b^{2}}{a b^{-2}(a^{-3} b^{2})^{3} a^{2} b^{3}}\)
1) Simplifier le nombre \(A\).
2) Calculer A pour: \(a=10^{-3}\) et \(b=-10^{-4}\).

Exercice 20:
Donner l’écriture scientifique de chacun des nombres suivants:
\(X=5× 10^{-2}+3× 10^{-3}\)
\(Y=\frac{132214× 10^{-3}-2140000× 10^{-7}}{3× 10^{10}}\)
Montrer que : \(2^{16}-1=(2^{8}+1)(2^{4}+1)(2^{2}+1)(2+1)\)

Exercice 21:
Déterminer l’entier \(n\) sachant que :
\(\frac{16^{n-4}× 2^{6 n+1}}{128^{n-3}}=4096\)
Déterminer un entier naturel a tel que :
\(2 a^{2}× a^{3}=6250\)

Exercice 22:
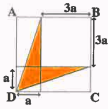
ABCD est un carré Calculer l’aire coloriée en fonction de a.

Devoir

Exercice 01:
1) Simplifier :
A=\((\frac{2}{5})^{-2} ×(-\frac{4}{25})^{-3} ×(-\frac{5}{2})^{-3}\)
B=\((a^{-4} b^{-1} c^{2})^{-3} ×[(a^{-2})^{3} × b^{-1}]^{-1}\)
2) Donner l’écriture scientifique de C:
C=\(\frac{12 × 10^{-46}-0,003 × 10^{-43}}{0,3 × 10^{-12}}\)

Exercice 02:
Effectuer les calculs suivants:
a=\(\frac{4}{3}-\frac{1}{12} × 4^{3}-6 ×(\frac{5}{3})^{2}\)
b=\(\frac{15 × 10^{6}(2 × 10^{-3})^{2}}{24 × 10^{3}}\)
c=\(\frac{a^{3} × b^{-1} × a^{2}}{(a^{2})^{2} ×(b^{-1})^{-2}}\)

Exercice 03:
1) Calculer \(x=(\frac{3}{5})^{-3} ×(\frac{2}{5})^{2} × \frac{2^{-7}}{5^{-2}}\)
2) On pose: \(\alpha=\frac{4 × 300^{2} ×(10^{-4})^{-2}}{(0,01)^{-3}}\)
a- Montrer que \(\alpha=36 × 10^{6}\)
b- Déterminer l’écriture scientifique de \(\alpha\).
3) Montrer \(28 × 6^{n}-6^{n+1}\) est un multiple de 11 .
(ou \(n\) est un entier naturel)
Exercice 04:
On donne : E =\(\frac{( a ^{3} b ^{-3})^{4}}{[( a ^{-2})^{-5} b ^{3}]^{-2}}\)
a- Montrer que : E =\(\frac{ a ^{32}}{ b ^{6}}\).
b- Calculer \(E\) lorsque : \(a =3 × 10^{-2} et b =27 × 10^{3}\)
c- Donner l’écriture scientifique de \(E\).

Exercice 05:
Calculer : a =\((\frac{9}{4})^{2018} ×(\frac{16}{36})^{2018}\)
b=\((\sqrt{17})^{8} ×(\sqrt{17})^{5}\)
c=\(\frac{2^{-5} × 8^{-3}}{a^{-16} × 2^{2}}\)

Exercice 06:
\(a\) et \(b\) sont deux nombres réels non nuls.
Simplifier E:
E=\(\frac{(a^{3} b)^{-3} ×(a b^{3})^{3} ×(a^{-2} b^{2})^{3}}{(a b^{-1})^{-2} ×(a^{-1} b^{2})^{3} × b^{-4}}\)

Exercice 07:
1) Calculer: \(a=[(\frac{5}{3})^{2}+(\frac{3}{7})^{-2}]^{-1}\)
2) Montrer que: \([\frac{(3 \sqrt{5})^{2}}{135}]^{-2}=9\)

Exercice 08:
1) Calculer :
\(a=(2^{-2}+\frac{3}{4})^{100}\)
\(b=2^{-2} ×(2,5)^{5} × 5^{-3} × 4^{5}\)
\(c=\frac{7^{-n+1} × 7^{n}}{7^{3 n}} ×(343)^{n}\).

Exercice 09:
1) Calculer :
a=\(\frac{1-(\frac{3}{4})^{-2}}{(\frac{\sqrt{7}}{3})^{2}}\)
2) b et c sont deux nombres réels tels que :
b =\(38,2 × 10^{4} \text { et } c =0,003 × 10^{8}\)
Donner l’écriture scientifique de b+c.

Exercice 10:
1) Calculer: \(a=\frac{3^{2} × 2^{-5} × 6^{-1}}{2^{-6} × 6^{2} × 3}\).
2) Simplifier
E=\(\frac{(b^{2})^{-1} × a^{7}}{a^{4} b^{-6} a^{-1} b^{5}}\)

Olympiade

Exercice 1:
Montrer qu’il n’existe pas d’entier naturel \(x\)
tel que: \(6× 4^{x}-7× 6^{x}+6× 9^{x}=0\)

Exercice 2:
Ranger les nombres dans l’ordre croissant : \(2^{100} ; 3^{75} ; 5^{50}\)
Quel est le chiffre des unités de \(3^{100}\) ?

Exercice 3:
Sachant que:
\(x^{2}+y^{2}=10\) et \(x^{3} y+x^{2} y^{2}+x y^{3}=39\).
Calculer \(x+y\)

Exercice 4:
Montrer que : \(5555555^{2}=4444444^{2}+3333333^{2}\)
Montrer que : \(499999^{2}+999999=25× 10^{10}\)

Exercice 5:
1) Démontrer que pour tout entier \(n: 2^{n}=2^{n+1}-2^{n}\).
2) En déduire une valeur de \(S\) :
\(S=2^{0}+2^{1}+2^{2}+\ldots+2^{49}+2^{50}\)

Exercice 6:
comparer \(x\), y et \(z\). Si : \(x^{3}=a^{4}\) et \(y^{4}=a^{3}\) et \(z^{6}=a^{7}\)

Exercice 7:
Déterminer l’entier relatif \(x\) tel que : \(\frac{15}{a^{x-2}}+a^{x-2}=16\)

Exercice 8:
a et b sont deux nombres réels tels que :
\(a^{4036}+b^{4036}=(a^{2}+b^{2})(a b)^{2017}\)
1) Montrer que : \((\frac{a}{b})^{2018}+(\frac{b}{a})^{2018}=\frac{a}{b}+\frac{b}{a}\).
2) En déduire que : \([(\frac{a}{b})^{2018}-\frac{a}{b}][1-(\frac{b}{a})^{2019}]=0\).