Calcul Littéral et Identités Remarquables 3ème collège Exercices

Entraînement

Série 1

Exercice 1
Effectuer sans utiliser la calculatrice :
A=10-8,5+2-3,5+3,7
B=125-949-53-17+74-9
C=3×(-5,5)× 10×(-5)×(-0,25)
D=0,7×(-8)×(-6)× 125

Exercice 2
Effectuer les calculs et écrire le résultat sous forme de fraction irréductible :
a=\((\frac{1}{10}-\frac{1}{4}): \frac{6}{5}-1\)
b=\(\frac{3}{8}-2×\frac{(14+4)}{(14-2)}\)
c=\(\frac{(2+4)^{2}-(4-8)^{2}}{17^{2}-16^{2}}\)
d=\(\frac{(3-8)^{2}-(2+6)^{2}}{(7+4)^{2}}\)

Exercice 3
Développer et réduire les expressions suivantes:
A=3a-(5a-6)+8+(-7-6a)
B=15+3a+(4 a-9)-(6-10a)
C=7 a+(-9a+8)-(-5 a-3)+12
D=3-[8-(4a+5)]+[-9-(-10+8a)]
E=-(3b-4)+3 a-[3a-(5b-5)]-(2a-3)
F=6b-\([\frac{7}{2}+(2 a+\frac{3}{2} b)]+[-\frac{9}{2}-(\frac{5}{2} a+\frac{9a}{2}-2)]\)

Exercice 4
Développer puis réduire les expressions suivantes :
A =\(3 x^{2}-(5-3 x+4 x^{2})+(7-2 x^{2})\)
B =\(4 x^{2}+(1-6 x^{2})+3 x^{2}+(2 x^{2}-5 x^{3})\)
C =\(8 x+(4 x^{3}-6 x+2 x^{2})+(2 x^{3}-x^{2})\)
D =\(7-(3 x^{2}-4 x-1)+(x^{2}-9 x-11)\)

Exercice 5
Développer et réduire :
A=\(3x(x-2)-2 x(3x-2)\)
B=\(4-2(5-x)+6 x^{2}-3x(3 x-2)\)
C=\(7x+x(-3x+2)-4 x^{2}+8 x(2+3x)\)
D =\(x^{2}(x^{2}-x-1)-x(3 x-5)+2(x^{3}-x-2)-9\)

Exercice 6
Ecrire chacune des expressions suivantes sous la forme \(ax + b\) :
A =\(\frac{3}{8} x-\frac{7}{4}-(\frac{5}{2} x+1)-\frac{1}{2}(3 x-\frac{5}{8})\)
B =\(\frac{2 x}{9}-1-\frac{x+3}{3}+\frac{x}{6}\)
C =\(\frac{x+2}{6}+\frac{2 x+3}{4}+\frac{3-2 x}{2}\)
D =\(\frac{2 x-1}{5}-\frac{x-2}{15}-\frac{x+1}{3}\)

Exercice 7
Développer :
A=\((3x-1)^{2}\)
B =\((3+4x)^{2}\)
C=\((\frac{2}{5} x+1)^{2}\)
D=\((\frac{5}{3} x-\frac{1}{2})^{2}\)
E =\((10-11 x)(10+11 x)\)
F =\((\frac{7}{8}+\frac{3}{5} x)(\frac{7}{8}-\frac{3}{5} x)\)

Exercice 8
Développer et réduire les expressions suivantes :
A =\((\frac{2}{5} x-5)^{2}-(\frac{x}{5}-\frac{1}{2})(\frac{x}{5}+\frac{1}{2})\)
B =\(\frac{4}{3} x(9 x+12)-(x+\frac{1}{3})^{2}\)
C =\(\frac{4}{3} x-1)(4 x+1)+(2 x-\frac{1}{4})^{2}\)
D =\((\frac{3x-2}{6})^{2}-(\frac{2 x+1}{2})^{2}\)
E =\((\frac{2}{5} x+1)^{2}-\frac{4}{25}(10+\frac{x}{2})^{2}+\frac{x}{10}(7+4x)\)

Série 2

Exercice 9
Développer et réduire les expressions suivantes :
E =\(x( y -2)+ y (2-x)+2(x- y)\)
F =\((x- y )( y -2)+( y -2)(2-x)+(2-x)(x- y)\)

Exercice 10
Donner la forme réduite de chacune des expressions suivantes:
A =\((2x-1)(x-4)+(3-x)(2 x+1)\)
B =\((x-2)(3 x-2)-(x+2)(2 x-3)\)
C =\(2(4-3 x)(2-3 x)-(x-2)(x-4)\)
D =\(5-[5-3 x(x-3)]+(2 x+3)(3 x+2)\)
E =\(3 x(x-2) x+1)-x(5 x-2)\)
F =\((x-2)^{2}-(3 x-1)(x-3)\)
G =\((x^{2}+x-1)^{2}\)
H =\((3x^{2}-x+2)(3 x^{2}+x-2)\)
I =\((-2 x+1)^{3}-(x-1)(x+2)(x-3)\)

Exercice 11
Factoriser chacune des expressions suivantes :
A =\((x+4)(6x-1)+(x+4)(7x-2)\)
B =\((2x+1)(x-5)-(2x+1)(4x+7)\)
C =\((3 x-5)(2 x-1)-(5-3x)(x+6)\)
D =\((x-2)(-x+3)+(2x-4)(3x-7)\)
E =\((6x+5)(x+8)-(6x+5)^{2}\)
F =\((5x-2)(x+3)-(2-5x)^{2}\)
G =\((x+9)(2 x-1)-6x^{2}+3x\)

Exercice 12
Factoriser les expressions suivantes :
A =\(x^{2}-14 x+49\)
B =\(4 x^{2}-24 x+36\)
C =\(45x^{2}-120 x+80\)
D =\(25x^{2}+40 x+16\)
E =\(4+9 x^{2}-12 x\)
F =\(16 x^{2}-81\)

Exercice 13
Factoriser les expressions suivantes :
A =\((x-3)(6x-7)-(x^{2}-6x+9)\)
B =\((2x-5)^{2}-9\)
C =\((3x+1)^{2}-x^{2}-x-\frac{1}{4}\)
D =\(4x^{2}+4 x+1-(x+5)^{2}\)
E =\(-(3-2 x)^{2}+(2 x-3)(x-5)+4 x-6\)
F =\((x+2)^{2}-2(x+2)(5 x-1)+(5x-1)^{2}\)
G =\(4 x^{2}-4+(5 x+1)(x-1)+2 x^{2}-4x+2\)

Exercice 14
Recopier et compléter pour que chaque égalité soit vraie :
\((5x-1)(3 x+2)=\ldots x^{2}+\ldots x-2\)
\((2x-\ldots .)(x+\ldots . .)=\ldots \ldots-x-3\)
\((x-4)(\ldots x+\ldots)=2 x^{2}-5 x-12\)
\((x+\ldots)(\ldots x-6)=4 x^{2}+6 x-18\)

Exercice 15
Recopier et compléter pour que chaque égalité soit vraie :
\((x+\ldots)^{2}=\ldots+8 x+\ldots\)
\((\ldots-\ldots)^{2}=9 x^{2}-\ldots+49\)
\((5 x-\ldots)(\ldots+\ldots)=\ldots-9\)
\((2x+\ldots)^{2}=\ldots+\ldots+36\)

Exercice 16
Recopier et compléter pour que chaque égalité soit vraie.
\(36x^{2}-\ldots=(\ldots-5)(\ldots+5)\)
\(\ldots+6x+\ldots=(x+\ldots)^{2}\)
\(\ldots-54x+81=(\ldots-\ldots)^{2}\)
\(4x^{2}-\ldots+9=(\ldots-\ldots)^{2}\)
\(\ldots-49=(\ldots-7)(3x+\ldots)\)

Approfondissement

Exercice 1:
Factoriser chacune des expressions suivantes:
A=(2 x+1)(x-5)-(2 x+1)(4 x+7)
B=(3 x-5)(2 x-1)-(5-3 x)(x+6)
C=(x-2)(-x+3)+(2 x-4)(3 x-7)
D=(6 x+5)(x+8)-(6 x+5)^{2}
E=(5 x-2)(x+3)-(2-5 x)^{2}
F=(x+9)(2 x-1)-6 x^{2}+3 x

Exercice 2 :
On donne: \(A=x^{2}-7 x+10\)
1) Montrer que : \(x^{2}-7 x+10=(x-\frac{7}{2})^{2}-\frac{9}{4}\)
2) Factoriser \(A\).

Exercice 3 :
Montrer les égalités suivantes:
\((x+y)^{2}-(x-y)^{2}=4 x y\)
\((x+y)^{2}+(x-y)^{2}=2(x^{2}+y^{2})\)
\(x^{2}-y^{2}-2 y-1=(x+y+1)(x-y-1)\)
\((x^{2}+1)(y^{2}+1)=(x y+1)^{2}+(y-x)^{2}\)
\((x^{2}-1)(y^{2}-1)=(x y+1)^{2}-(y+x)^{2}\)

Exercice 4 :
Développer et réduire les expressions suivantes:
E=\(x(y-2)+y(2-x)+2(x-y)\)
F=\((x-y)(y-2)+(y-2)(2-x)+(2-x)(x-y)\)

Exercice 5:
1) Montrer les égalités:
\(4^{2}+4=5^{2}-5 ; 16^{2}+16=17^{2}-17\)
\(119^{2}+119=120^{2}-120\)
2) Enoncer le résultat général et le démontrer.

Exercice 6:
\(x\) est un entier naturel.
1) Montrer que: \((x-1) x(x+1)+x=x^{3}\)
2) En déduire que \(102× 103× 104+103\) est un cube

Exercice 7:
A=\((x-4)^{2}-(x-2)(x-8)\)
I) Développer et réduire \(A\) :
2) En déduire le résultat de \(9996^{2}-9998× 9992\).

Exercice 8:
1) Calculer: \(69^{2}-68^{2}-67^{2}+66^{2}\)
2) a. \(x\) est un entier naturel.
Développer et réduire l’expression \(A\) :
A=\((x+3)^{2}-(x+2)^{2}-(x+1)^{2}+x^{2}\)
b. En déduire le calcul de :
B=\([(987654321258)^{2}+(987654321255)^{2}]-[(987654321257)^{2}+(987654321256)^{2}]\)

Exercice 9:
Soit \(x\) un nombre réel.
On donne : \(E=(2 x+1)^{2}-(2 x-1)^{2}\)
1) Développer et réduire \(E\).
2) En déduire la valeur de \(2019^{2}-2017^{2}\)

Exercice 10 :
On donne: \(E=1000002000001\)
Montrer que E est un carré parfait.

Exercice 11:
1) On a: \(13^{2}=169\); donc \(14^{2}=169+13+14=196\).
Calculer de la même manière \(15^{2}, 16^{2}, 17^{2}\).
2) Enoncer le résultat général et le démontrer.

Devoir

Exercice 1:
Calculer et donner le résultat sous forme d’une fraction irréductible:
A=\(\frac{1}{2}× \frac{1}{2}-\frac{5}{4}× \frac{1}{3}\)
B=\(\frac{\frac{1}{3}-\frac{3}{4}}{\frac{1}{4}-\frac{4}{3}}\)
C=\((\frac{3}{4}-\frac{5}{8})-[\frac{7}{6}-(\frac{3}{2}-2)]\)

Exercice 2:
Calculer et donner le résultat sous forme d’une fraction irréductible la plus simple possible:
A=\((1-\frac{4}{5}): \frac{3}{10}\)
B=\((\frac{1}{8}-\frac{3}{6})×(\frac{5}{12}-\frac{1}{4})\)
C=\(\frac{9}{3}-\frac{1}{3}×(\frac{5}{6}-1)\)

Exercice 3:
Calculer et donner le résultat sous la forme d’une fraction irréductible :
A =\((\frac{36}{-14})× \frac{70}{24}×(\frac{-4}{5})\)
B =\(\frac{\frac{4}{7}-\frac{3}{14}}{-\frac{4}{3}-\frac{5}{3}× \frac{1}{2}}\)

Exercice 4:
\(x\) est un nombre réel.
On donne: \(A=(x-3)^{2}-1 \quad\) et \(B=3 x^{2}+3 x-18\)
1) Factoriser \(A\).
2) Calculer A – \(\frac{1}{3}\) B.
3) En déduire la forme factorisée de \(B\).

Exercice 5:
On considère l’expression \(\mathrm{A}: A=6 x^{2}-5 x+1-(4 x-2)(x+1)\)
1)a. Développer et réduire \(A\).
b. Calculer A lorsque \(x=-\frac{2}{3}\)
2) a. Développer \((2 x-1)(3 x-1)\)
b. Factoriser \(A\).
c. Calculer A lorsque \(x=-\frac{1}{3}\).

Exercice 6:
Soit \(x\) un nombre réel.
On donne: \(E=(x+1)^{2}-(x-1)^{2}\)
1) Développer \(E\).
2) En déduire la valeur de \(F: F=10001^{2}-9999^{2}\)

Exercice 7:
On considère les expression suivantes:
A=(3 x-2)(x+2)-(3 x-2)(4 x-1)
B=(x+2)^{2}-9
1)a. Développer et réduire \(A\) et \(B\).
b. Calculer A pour \(x=\frac{-4}{3}\)
2) a. Factoriser \(A\) et \(B\).
\(b\). En déduire que : \(A-B=(x-1)(1-10 x)\).

Exercice 8:
I) Compléter:
\(4× 5× 6+5=(\ldots)^{3}\)
\(7× 8× 9+8=(\ldots)^{3}\)
\(21× 22× 23+22=(\ldots)^{3}\)
2) La somme du produit de trois nombres entiers consécutifs
plus le terme médian est égale à ce nombre. Est – ce toujours vrai?

Olympiade

Exercice 1:
\(a, b\) et c sont des nombres réels non nuls
tels que: \(a b+b c+c a=a b c\).
Calculer:
\(\frac{a+b}{a b}+\frac{b+c}{b c}+\frac{c+a}{c a}\)

Exercice 2:
\(x\) et \(y\) sont deux nombres recels distincts
tels que: \(x^{2}+y^{2}=3 x y\).
Déterminer la valeur de l’expression : \(A=\frac{x+y}{x-y}\).

Exercice 3:
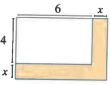
Les dimensions d’un rectangle sont \(6 m\) et \(4 m\).
On augmente la longueur et la largeur de \(x\) mètres.
Calculer, en fonction de \(x\), le périmètre p et l’aire \(S\) de la partie Colorée.

Exercice 4:
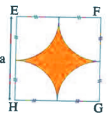
EFGH est un carre de coté a .
Soit \(S\) l’aire de la partie Colorée.
Montrer que : \(S=(1-\frac{\pi}{4}) a^{2}\)

Exercice 5:
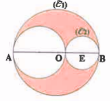
Dans la figure ci-contre :
\(C_{1}(O ; R), C_{2}(E ; x)\) et \([A B]\) est un diamètre de 1.
Calculer l’aire \(S\) de la partie Colorée en fonction de \(\pi\), R et \(x\)

Exercice 6:
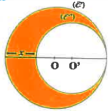
(C) est un cercle de centre \(O\) et de rayon \(R\).
(C) est un cercle de centre \(O ^{\prime}\) et tangente à \((C)\) (voir la figure).
Calculer l’aire \(S\) de la partie Colorée en fonction de \(R\) et \(x\).

Exercice 7:
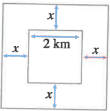
Un agriculteur veut entourer son champ de forme carrée
dont la longueur de son côté est \(2 km\) par une bande de largeur \(x\).
Sachant que l’aire de la bande est égale a l’aire du champ.
Déterminer alors la largeur \(x\) de la bande.

Exercice 8:
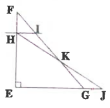
EFG est un triangle rectangle isocèle en E
tel que : EF = 6cm. On donne : FH = a. 
J est un point de la droite (EG) tel que GE[EJ] et JG = a. 
Montrer que KIH et KGI ont même aire . 

Exercice 9:
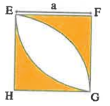
EFGH est un carné de côté a.
Calculer l’aire \(S\) de la partie Colorée en fonction de a.