Exercice 1: (10 Pts)
A-
1-Verifier que ∀x∈IR+ :
\(0≤ 1-x+x^{2}-\frac{1}{x+1}≤ x^{3}\)
2. En déduire que ∀x∈IR+ :
\( 0≤ x-\frac{x^{2}}{2}+\frac{x^{3}}{3}-\ln (1+x)≤ \frac{x^{4}}{4}\)
B- On considère la fonction \(f\)
définie sur I=[0,+∞[ par \(f(0)=\frac{1}{2}\):
\(∀x∈[0,+∞[; (f(x)=\frac{x-\ln (1+x)}{x^{2}}\)
et soit \((C)\) sa courbe représentative
dans un repère orthonormé \((O,\vec{i}, \vec{j})\)
1-a) Montrer que: \(f\) est continue d droite en 0
b) Montrer que: \(f\) est dérivable a droite en 0
c) Calculer \(\lim _{x⟶+∞} f(x)\),
puis interpréter graphiquement le résultat obtenu.
2-a) Montrer que ∀ x∈] 0,+∞[:
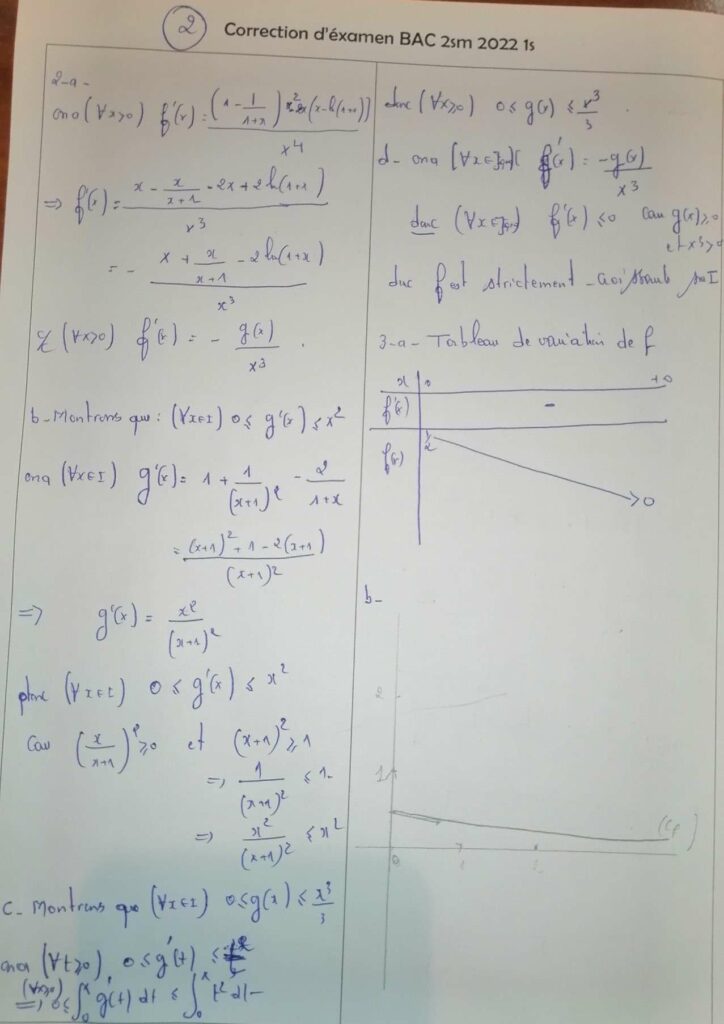
\(f^{\prime}(x)=-\frac{g(x)}{x^{3}}\)
ou \(g(x)=x+\frac{x}{x+1}-2 \ln (1+x)\)
b) Montrer que ∀ x∈ I) :
\(0≤ g^{\prime}(x)≤ x^{2}\)
c) En déduire que ∀ x∈ I:
\(0≤ g(x)≤ \frac{x^{3}}{3}\)
d) Déterminer le sens de variation de \(f\) sur \(I\)
3-a) Dresser le tableau de variation de \(f\)
b) Représenter graphiquement la courbe \((C)\)
dans le repère \((O, \vec{i}, \vec{j})\)
(On prendra \(\|\vec{j}\|=2cm\) et \(\|\vec{j}\|=2cm\))
C-
1- Montrer qu’il existe un unique réel \(α\)∈]0;1[
tel que:\(f(α)=α\)
2- On considère la suite \((u_{n})_{n∈IN}\) définie par:
\(u_{0}=\frac{1}{3}\)
et ∀n∈IN: \(u_{n+1}=f(u_{n})\)
a) Montrer que ∀\(n\)∈IN : \(u_{n}∈[0;1]\)
b) Montrer que ∀ \(n\)∈IN:
\(|u_{n+1}-α|≤(\frac{1}{3})|u_{n}-α|\)
c) Montrer par récurrence que ∀ n∈IN:
\(|u_{n}-a|≤(\frac{1}{3})^{n}\)
d) En déduire que:
la suite \((u_{n})_{n∈IN}\) converge vers \(α\)
D-
Pour tout \(x∈I\), on pose:
\(F(x)=\int_{2}^{1} f(t) dt\)
1- Montrer que: la fonction \(F\) est dérivable sur \(l\)
et calculer \(F^{\prime}(x)\) pour tout \(x∈ I\)
2-a) En utilisant la méthode d’intégration par parties,
montrer que ∀ \(x∈[0,+∞[\):\(F(x)=2 \ln 2-(1+\frac{1}{x}) \ln (1+x)\)
b) Calculer \(\lim _{x⟶ 0^{+}} F(x)\),
puis en déduire que.:
\(\int_{0}^{1} f(t) dt=2 \ln 2-1\)
c) Calculer en \({cm}^{2}\).
l’aire du domaine plan limite par la courbe \((C)\).
l’axe des abscisses. l’axe des ordonnés el la droite d’équation \(x=1\)
E-
On pose, pour tout \(k\) de IN :
\(Δ_{k}=f(k)-\int_{k}^{k+1} f(t) dt\)et pour tout \(n\) de IN*:
\(S_{n}=\sum_{k=0}^{1=n-1} Δ_{k}\)
1-a) Vérifier que ∀ \(k\) ∈ IN: \(0≤ Δ_{k}≤ f(k)-f(k+1)\)
b) En déduire que ∀ \(n\) ∈ IN*: \(0≤ S_{n}≤ \frac{1}{2}\)
2-a) Montrer que la suite \((S_{n})_{n∈ IN^{*}}\) est monotone.
b) En déduire que la suite \((S_{n})_{n∈ IN^{*}}\) est convergente.
c) Montrer que:
la limite \(\ell\) de la suite \((S_{n})_{n∈ IN^{*}}\)
vérifie:\(\frac{3}{2}-2 \ln 2≤ \ell≤ \frac{1}{2}\)
Correction




EXERCICE 2: (3.5 points)
Soit \(m\) un nombre complexe non nul donné
et \(j=-\frac{1}{2}+\frac{\sqrt{3}}{2} i\)=\(e^{t \frac{2 x}{3}}\)I-
On considère dans l’ensemble \(C\) l’équation d’inconnue \(z\)
\((E_{m}): z^{2}+m j^{2} z+m^{2} j=0\)
1- Vérifier que:
\(j^{3}=1\) et \(1+j+j^{2}=0\)
2-a) Montrer que:
le discriminant de l’équation \((E_{m})\) est \(Δ=[m(1-j)]^{2}\)
b) Déterminer \(z_{1}\) ef \(z_{2}\)
les deux solutions de l’équation \((E_{m})\)
3- Dans cette question, on suppose que, \(m=1+i\)
Montrer que:
\((z_{1}+z_{2})^{2022}\) est un imaginaire pur.
II-
Le plan complexe est muni d’un repère
orthonormé direct \((O, \vec{u}, \vec{v})\).
Soit \(φ\) la transformation du plan complexe qui de tout point \(M(z)\)
fait correspondre le point \(M^{\prime}(z^{\prime})\)
tel que: \(z^{\prime}=(1+j) z\)
1- Déterminer:
la nature el les éléments caractéristiques de l’application \(φ\)
2- On considère les points \(A, B\) et \(C\)
d’affixes respectives \(m\). \(m j\) et \(m j^{2}\)
et on note \(A^{\prime}(a^{\prime}) \cdot B^{\prime}(b^{\prime})\) et \(C^{\prime}(c^{\prime})\) les images respectives
des points \(A . B\) el \(C\) par l’application \(φ\) el soient \(P(p), Q(q)\) cl \(R(r)\) les milieux respectifs des segments \([BA^{\prime}] \cdot[CB^{\prime}]\) et \([AC^{\prime}]\)
a) Montrer que:
\(a^{\prime}=-m j^{2}, b^{\prime}=-m\) et \(c^{\prime}=-m j\)
b) Montrer que:
\(p+q j+r j^{2}=0\)
c) En déduire que:
le triangle \(PQR\) est équilatéral.
Correction


EXERCICE3 , ( 3 points)
Soit \(n\) un entier naturel strictement supérieur \(\dot{1} \mid\)
On considère dans \(N^{2}\) l’équation :
\((E_{n}): (x+1)^{n}-x^{n}=m y\)
Soit \((x, y)\) une solution de l’équation \((E_{a})\) dans \(IN^{2}\)
et soit \(p\) le plus petit diviseur premier de \(n\)
1-a) Montrer que:
\((x+1)^{n} ≡ x^{n}[p]\)
b) Montrer que:
\(p\) est premier avec \(x\) et avec \((x+1)\)
c) En déduire que:
\((x+1)^{p-1} ≡ x^{p-1}[p]\)
2- Montrer que:
si \(n\) est pair, alors l’équation \((E_{n})\) n’admet pas de solution dans \({IN}^{2}\)
3- On suppose que \(n\) est impair.a) Montrer que:
il existe un couple \((u,v)\) de \(Z^{2}\)
tel que \(nu+(p-1)v=1\)
(On rappelle que \(p\) est le plus petit diviseur premier de \(n\) )
b) Soient \(q\) et \(r\) respectivement
le quotient et le reste dans la division euclidienne de \(n\) par (p-1)\).
Vérifier que: \(nr=1-(p-1)(v+nq)\)
c) On pose, \(v^{\prime}=-(v+nq)\).
Montrer que: \(v^{\prime} \geq 0\)
d) Montrer que:
L’équation \((E_{n})\) n’admet pas de solution dars \(\mathrm{N}^{2}\)
Correction


EXERCICE 4 ( 3.5 points)
On rappelle que \((M_{2}(IR),+, ×)\) cst un anneau unitaire non commutatif d’unité
\(I=(\begin{array}{ll}1 & 0 \\ 0 & 1\end{array})\)
et que \(({Z}_{,}+, x)\) est un anneau commutatif unitaire et intègre.
Soit
\(E=\{M(a, b)=(\begin{array}{ll}a & 3 b \\ b & a\end{array}) /(a, b)∈ \mathbb{Z}^{2}\}\)
1-a) Montrer que:
\(E\) esl un sous-groupe de \((M_{2}(\mathrm{R}),+)\)
b) Vérifier que:
pour tout \(a, b, c\) et \(d\) de \(\mathrm{Z}\), on a
\(M(a, b)× M(c, d)=M(a c+3 b d, a d+b c)\)
c) Montrer que:
\((E,+, ×)\) cst un anneau commutatif et unitaire.
2- Soit\(φ\) l’application définie de \(E\) vers \(Z\) par:
\(∀(a, b)∈ \mathbb{Z}^{2} ; φ(M(a, b))=|a^{2}-3 b^{2}|\)
Montrer que:
\(φ\) est un homomorphisme de \((E,×)\) vers \((\mathbb{Z}, ×)\)
3- Soit \(M(a, b)∈ E\)
a) Montrer que \(M(a, b)× M(a,-b)=(a^{2}-3 b^{2}) . I\)
b) Montrer que:
si \(M(a, b)\) est inversible dans \((E,×)\) alors \(φ(M(a, b))=1\)
c) On suppose que \(φ(M(a, b))=1\).
Montrer que:
\(M(a, b)\) est inversible dans \((E, ×)\) et préciser son inverse.
4-a) Montrer que:
\(∀(a, b)∈{Z}^{2} ; φ(M(a, b))=0 ⇔ a=b=0\)
b) En déduire que: l’anneau \((E,+, ×)\) est intègre.
c) Est-ce que \((E,+, x)\) est un corps ? justifier votre réponse.
Correction




