Concours d’accès en 1ère année du cycle d’ingénieur ENSA 2018
Durée: 1h 30 mn
Remarques importantes:
– Une seule proposition est correcte par question:
Réponse juste = 1 point;
Réponse frusse =-1 point;
Plus d’une réponse cochée =-1 point;
Pas de réponse =0 point.
Q1:
((u_{n})) une suite réelle.
Si (lim _{n ➝+∞}(u_{n+1}-u_{n})=2),
alors (lim _{n ➝+∞} frac{u_{n}}{n}=)
A) 0
B) 1
C) +∞
D) 2
Q2:
(lim _{n ➝+∞} frac{sin ^{2} n-cos ^{3} n}{n}=)
A) 0
B) 1
C) -∞
D) +∞
Q3:
(lim _{x ➝ 1^{+}} ×ln xln (ln x)=)
A) 1
B) 0
C) +∞
D) -∞
Q4:
Soit ((u_{n})) la suite définie sur IN* par:
(u_{n}=sum_{k=1}^{n} frac{1}{k})
A) (u_{2 n}-u_{n} ≥ frac{1}{2})
B) (u_{2 n}-u_{n}≤ frac{1}{4})
C) (u_{2 n}-u_{n}<frac{1}{3})
D) (u_{2 n}-u_{n}<frac{1}{2})
Q5:
Pour la même suite que Q4.
Soit ((u_{n})) la suite définie sur IN* par:
(u_{n}=sum_{k=1}^{n} frac{1}{k})
On a:
A) (u_{2^{10}} ≥ 6)
B) (u_{2^{10}}<6)
C) (u_{2^{10}}=3)
D) (u_{2^{10}}<5 .)
Q6:
(cos (Arctan(x))=)
A) (frac{1}{sqrt{1-x^{2}}})
B) (frac{1}{sqrt{1+x^{2}}})
C) (frac{-1}{sqrt{1+x^{2}}})
D) (frac{-1}{sqrt{1-x^{2}}})
Q7:
Soit (f: IR ➝ IR ) une fonction continue en 0 telle que:
(∀x∈IR quad f(2x)=f(x)) Alors (f) est:
A) Constante
B) Strictement croissante
C) Strictement décroissante
D) périodique de période 2
Q8:
(f: IR ➝ IR ) une fonction dérivable en (a∈IR).
(lim _{x ➝ a} frac{x f(a)-a f(x)}{x-a}=)
A) f ‘(a)
B) f(a)+af ‘(a)
C) f(a)-f ‘(a)
D) f(a)-af ‘(a)
Q9:
(int_{0}^{1} frac{x^{4}}{x^{2}+1} dx=)
A) (frac{pi}{4})
B) (frac{2}{3})
C) (frac{pi}{4}-frac{2}{3})
D) (frac{pi}{4}+frac{2}{3})
Q10:
(int_{0}^{sqrt{3}} x^{2} ln (x^{2}+1) d x=)
A) (sqrt{3} ln 2-frac{pi}{9})
B) (sqrt{3} ln 2+frac{pi}{9})
C) (2(sqrt{3} ln 2-frac{pi}{9}))
D) (sqrt{3} ln 2)
Exercice 1:
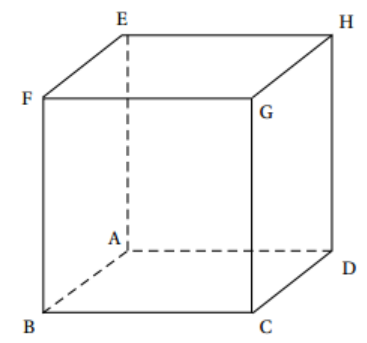
On considére la cube ABCDEFGH
et on note
(A,overrightarrow{AB},overrightarrow{AD},overrightarrow{AE}) un repère orthonormé de l’espace.
Q11:
Les coordonnées du vecteur (overrightarrow{FD}) sont
A) (1,1,1)
B) (-1,1,1)
C) (-1,1,-1)
D) (1,1,0)
Q12:
Une représentation paramétrique de la droite (FD)
A) (left{begin{array}{c}x=t \ y=t+1, \ z=-tend{array}right.) (t∈R)
B) (left{begin{array}{c}x=-t \ y=-t+1, \ z=-tend{array}right.) (t∈R)
C) (left{begin{array}{c}x=-t \ y=t+1, \ z=-tend{array}right.) (t∈R)
D) (left{begin{array}{c}x=t \ y=t+1, \ z=+tend{array}right.) (t∈R)
Q13:
On note I le milieu du segment [AB], J le milieu du segment [EH] et K le milieu du segment [BC]. La droite (FD)
A) est orthogonale au plan (IJK)
B) n’est pas orthogonale au plan (IJK)
C) appartient au plan (IJK)
D) paralléle au plan (IJK)
Q14:
Une équation cartésienne du plan (IJK) est ax + by + cz +d =0 avec
A) a=-1, b=-1, c=1 et d=-(frac{1}{2})
B) a=1, b=-1, c=1 et d=-(frac{1}{2})
C) a=-1, b=-1, c=1 et d=(frac{1}{2})
D) a=1, b=1, c=-1 et d=-(frac{1}{2})
Q15:
Les coordonnées du point M; intersection de la droite (FD) et le plan (IJK) sont:
A) ((frac{1}{2}),(frac{1}{2}),(frac{1}{2}))
B) ((frac{1}{2}),0,(frac{1}{2}))
C) ((frac{1}{2}),(frac{1}{2}),0)
D) (1,1,0)
Q16:
Le triangle IJK est
A) Équilatéral
B) Rectangle en J
C) Rectangle en K
D) Rectangle en I
Exercice 12:
Le QCM du concours ENSA comporte 20 questions, pour chacune desquelles 4 réponses sont proposées et une seule est correcte.
Un étudiant décide de remplir la grille-réponses en cochant au hasard une réponse pour chacune des 20 questions. Pour n∈IN et (0≤ n≤ 20),
on note (A_{n})
» répondre au hasard exactement n fois correctement »
l’évènement (A_{n}) est réalisé si n réponses sont correctes et (20-n) sont incorrectes.
((begin{array}{c}n \ pend{array})) désigne le nombre de combinaison de p parmi n.
Q17:
La probabilité de ne donner aucune réponse correcte est (P(A_{0})=)
A) (frac{3^{20}}{4^{20}})
B) (frac{24}{4^{20}})
C) (frac{1}{20^{4}})
D) (frac{1}{80})
Q19:
La probabilité de répondre au hasard au moins 6 fois correctement est
A) (sum_{n=6}^{20} frac{(begin{array}{c}20 \ nend{array}) 3^{20-n}}{4^{20}})
B) (sum_{n=0}^{6} frac{(begin{array}{c}20 \ nend{array}) 3^{20-n}}{4^{20}})
C)(sum_{n=6}^{20} frac{(begin{array}{c}20 \ nend{array}) 3^{20-n}}{20^{4}})
D) (sum_{n=0}^{6} frac{(begin{array}{c}20 \ nend{array}) 3^{20-n}}{20^{4}})
Q18:
La probabilité de donner exactement n bonnes réponses correctes est (P(A_{n})=)
A) (frac{(begin{array}{c}20 \ nend{array}) 3^{n}}{4^{20}})
B) (frac{(begin{array}{l}20 \ nend{array}) 3^{20-n}}{4^{20}})
C) (frac{(begin{array}{c}20 \ 3end{array})^{20-n}}{20^{4}})
D) (frac{(begin{array}{c}20 \ 3end{array}) 3^{n}}{80})
Correction Concours ENSA 2018:






