Exercice ① ( 4 points )
Soit \(a\) un réel non nul tel que: \(a^3 + \frac{1}{a^3}=18\)
Que vaut : \(a^4 + \frac{1}{a^4}\)
Exercice ② ( 4 points )
Trouver tous les entiers \(n\):
Soient \(a,b\) des réels tel que: \(a,b >1\)
Montrer que \(\frac{a^{2}}{b-1}+\frac{b^{2}}{a-1}≥8\)
Exercice ④ ( 4 points )
Soient \(x,y,z\) trois réels tels que :
\(x + y + z = 3\) et \(x ² +y ² + z ² = 4\)
Quelle est la plus grande valeur possible de z?
Lorsque \(z\) est égal à l’une de ces valeurs,
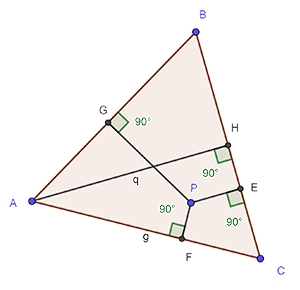
E,F et G sont les projetés orthogonaux respectifs du point P
sur les droites (CB), (CA) et (AB)
et H est le pied de la hauteur issue de A.
Montrer que: PE+PF+PG = AH
Soit \(a\) un réel non nul tel que: \(a^3+\frac{1}{a^3}=18\)
*On calcule x
On a \(x³ =(a+\frac{1}{a})^3\)
⇔\(x³=a³+\frac{1}{a³}+3\frac{1}{a²}a+3\frac{1}{a}a²\)
⇔x³=18 + 3x
(car \(a³+\frac{1}{a³}=18\))
Ainsi, On obtenons l’équation
la seule solution réelle est x=3
Le polynôme restant est x²+3x+6 n’a pas de racine réelle.
*On calcule \(a² +\frac{1}{a²}\)
Ainsi on a: \(x²=(a + \frac{1}{a})²\)
⇔\(9= a^2 + \frac{1}{a²} + 2\)
D’où \(a² +\frac{1}{a²}=7 \) ⓐ
*On calcule \(a⁴ +\frac{1}{a⁴}\)
ⓐ² ⇔ \((a² +\frac{1}{a²})² =7²\)
⇔ \(a⁴ +2+\frac{1}{a⁴} =49\)
⇔ \(a⁴+\frac{1}{a⁴} =49-2\)
Donc \(a⁴+\frac{1}{a⁴} =47\). Exercice ②
pour n=0: \(2^0+1\)=2 (0 n’est pas une solution)
Soit n∊IN* :
on a :
\(2^n+1\) est le cube d’un entier
⇔ s’il existe m∊IN tel que \(2^n+1=m^3-1\)
⇔ \(2^n=m^3-1\) ⇔ \(2^n=(m-1)(m²+m+1)\) ⓐ
*Si m est pair m=2p:
\(2^n=m^3-1=8p^3-1=impaire\)
(contradiction \(2^n\) est paire n>0)
*Si m est impair m=2p+1:
On a (m-1) et (m²+m+1) sont des puissances de 2 d’après ⓐ
(m²+m+1)=((2p+1)²+(2p+1)+1)=4p²+6p+3 est paire
(contradiction )
On en conclut donc qu’il n’existe pas de solutions.
Soient \(a,b\) des réels tel que: \(a,b >1\)
Montrer que \(\frac{a^{2}}{b-1}+\frac{b^{2}}{a-1}≥8\)
(x-2)² ≥ 0 ⇔ x²-4x+4 ≥ 0⇔x² ≥ 4(x-1)
pour x=a
a² ≥ 4(a-1) ⇔ \(\frac{a²}{b-1} ≥ 4\frac{a-1}{b-1}\) ⓐ (car b-1 > 0)
pour x=b
b² ≥ 4(b-1) ⇔ \(\frac{b²}{a-1} ≥ 4\frac{b-1}{a-1}\) ⓑ (car a-1 > 0)
ⓐ+ⓑ ⇔\(\frac{a²}{b-1}+\frac{b²}{a-1} ≥ 4(\frac{a-1}{b-1}+\frac{b-1}{a-1})\) ⓒ
d’autre part on a:
soit y > 0
(y-1)² ≥0⇔y²-2y+1 ≥ 0 ⇔ y²+1 ≥ 2y⇔y+\(\frac{1}{y} ≥ 2\)
on prend y=\(\frac{a-1}{b-1}\)
⇒ \(\frac{1}{y}=\frac{b-1}{a-1}\)
Alors \(\frac{a-1}{b-1}+\frac{b-1}{a-1} ≥ 2\)
Donc d’après ⓒ:
\(\frac{a²}{b-1}+\frac{b²}{a-1} ≥ \frac{a-1}{b-1}+\frac{b-1}{a-1}\)
⇔ \(\frac{a²}{b-1}+\frac{b²}{a-1}≥ 4×2=8\).
\(x+y+z=3\) et \(x²+y²+z²=4\)
Quelle est la plus grande valeur possible de z
On a:
x+y+z=3 ⇒ (x+y)=3-z
x²+y²+z²=4 ⇒ x²+y²=4-z²
On calcule (x-y)² en fonction de z
(x-y)²=x²+y²-2xy=2x²+2y²-x²-2xy-y²
(x-y)²=x²+y²-(x+y)²=2(4-z²)-(3-z)²
(x-y)²=-3z²+6z-1
Les racines de -3x²+6x-1=0:
\(x= \frac{3 \pm \sqrt{3^2 – 3}}3 = 1 \pm \sqrt{\frac 23}\)
ce qui signifie que
x,y ∊IR ⇔ (x-y)²≥0 ⇔ -3z²+6z-1 ≥0
⇔ \(1-\sqrt{\frac 23} ≤z ≤1+\sqrt{\frac 23}\)
⇒ (x – y)²=0 ⇒ x=y
d’autre part on a: x+y+z=3
On trouve que les points atteignant les valeurs extrémales de z
sont atteintes Quand
(x, y) = \((1+\frac 1{\sqrt 6}, 1+\frac 1{\sqrt 6}),(1-\frac 1{\sqrt 6}, 1-\frac 1{\sqrt 6})\).
Montrer que: PE+PF+PG = AH
\(S_{ABC}\): Surface de ABC
On a: \(S_{ABC}=S_{APB}+S_{BPC}+S_{CPA}\) ⓐ
d’ autre part
ABC un triangle équilatéral
on pose: AB=AC=BC=x
d’ où:
\(S_{ABC}=\frac{AH×BC}{2}=\frac{AH×x}{2}\)
\(S_{APB}=\frac{PG×AB}{2}=\frac{PG×x}{2}\)
\(S_{BPC}=\frac{PE×BC}{2}=\frac{PE×x}{2}\)
\(S_{CPA}=\frac{PF×AC}{2}=\frac{PF×x}{2}\)
Alors:
ⓐ ⇔ \(\frac{AH×x}{2}=\frac{PG×x}{2}+\frac{PE×x}{2}+\frac{PF×x}{2}\)
⇔ \(\frac{AH×x}{2}=\frac{(PG+PE+PF)×x}{2}\)
⇔ AH=PG+PE+PF.
➲ Si vous souhaitez signaler une erreur merci de nous envoyer un commentaire