Olympiade de Mathématiques( compétition de mathématiques destinée aux élèves des lycées et collèges)Olympiade Math – Algèbre 03 – Exercice 04
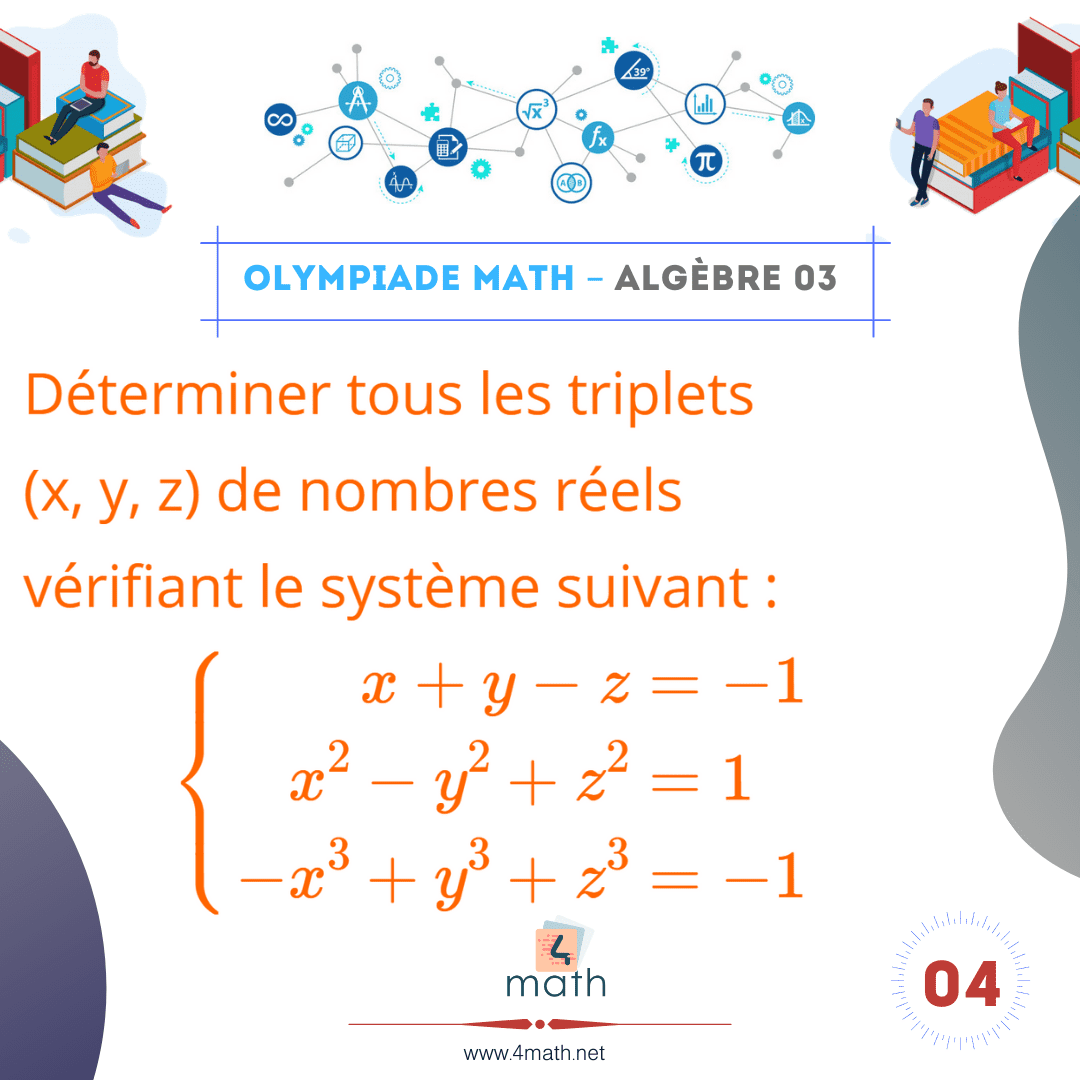
Déterminer tous les triplets (x, y, z) de nombres réels vérifiant le système suivant :
(left{begin{array}{ll} x+y-z=-1 \ x^{2}-y^{2}+z^{2}=1 \-x^{3}+y^{3}+z^{3}=-1 end{array}right.)
On a: x+y-z=-1 ①
x²-y ²+z²= 1 ②
-x³+y³+z³=-1 ③
①
x+y=z-1
Remplacer en suite dans ②
➝ (z − 1)(x − y + z + 1) = 0
➝ z = 1 ou x − y + z + 1 = 0
* Cas 1: z = 1 ➝ x = −y
En remplaçant dans ③
y = −1 et x = 1.
Donc (x,y,z) = (1,-1,1)
* Cas 2: x −y +z + 1 = 0
➝ z = −x+ y − 1
En remplaçant dans ①
➝ x = −1 ➝ z = y.
En remplaçant dans ③
➝ y = z = −1, Donc (x,y,z) = (-1,-1,-1).
Vérification des solutions.
(x,y,z) =(1,-1,1) , (-1,-1,-1).