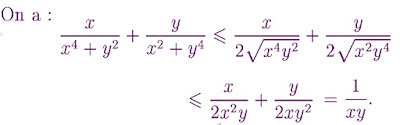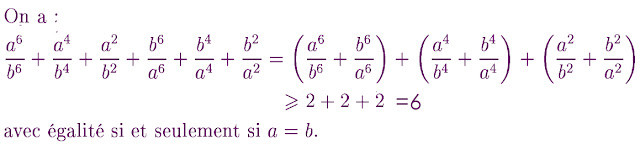Olympiade de Mathématique
( compétition de math destinée aux élèves des lycées et collèges)
Cours que nous vous proposons pour vous entraîner.
Cette évidence va nous servir à établir quelques résultats fort utiles.
Théorème 2: Un carré est toujours positif !
* Pour tous réels a, b, on a :
a²+b² ≥ 2ab et (a+b)² ≥ 4ab
avec égalité(s) si et seulement si a = b.
* Pout tout réel x > 0), on a : x + 1/x ≥ 2,
* Pour tous réels a, b, on a :
a²+b² ≥ 2ab et (a+b)² ≥ 4ab
avec égalité(s) si et seulement si a = b.
* Pout tout réel x > 0), on a : x + 1/x ≥ 2,
avec égalité si et seulement si x=1.
Application 1: (Russie 1995)
Prouver que pour tous réels x,y> 0:
Application 2:
Soient a, b deux réels non nuls.
Déterminer le minimum de:
Soient a, b deux réels non nuls.
Déterminer le minimum de:
Théorème 2: Un carré est toujours positif.Théorème 3: Inégalité de Cauchy-Schwarz.
Liens utiles :
L’Olympiade Internationale de Mathématiques (OIM)
Olympiade de Maths, c’est une gymnastique de l’esprit, Ce qu’il faut c’est 4 math .net et beaucoup de pratiques.
4 math .net Le première clé pour être bon en maths
4 math .net Le première clé pour être bon en maths