Olympiade Math – Géométrie 01 – Ex 18

Olympiade de Mathématiques
( compétition de math destinée aux élèves des lycées et collèges)


Olympiade Math – Géométrie 01 – Exercice 18

voir figure suivante:
(C) Cercle de rayon R.

 Calculer x,y en fonction de R ?

Voir solution


On considère les points A,B….E voir figure suivante:






* d’une part on a:
AE=8+y
AB=1/2AE=(8+y)/2
➝ CD=x+4

CF=1/2CD=(x+4)/2
BO=O’F=CF-CO’
➝ BO=(x+4)/2 – x=(4-x)/2

dans le triangle ABO:
AB²+BO²=AO²
(8+y)²/4+(4-x)²/4=R²
➝ (8+y)²+(4-x)²=4R² ➀

* d’autre part:
– CÔ’E=AÔ’D=90°.
– EC᳐O’ =DA᳐O’ (angles inscrits interceptant le même arc de cercle ont la même mesure).
➝ Les deux triangle O’CE & O’AD sent semblable:
➝ x/8=y/4
➝ x=2y.
➀↴
(8+y)²+(4-x)²=4R²
➝ (8+y)²+(4-2y)²=4R²
➝ 80+5y²=4R²
Donc:



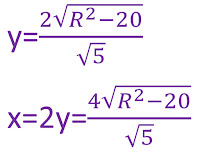
Liens utiles :
L’Olympiade Internationale de Mathématiques (OIM)
Olympiade de Maths, c’est une gymnastique de l’esprit, Ce qu’il faut c’est 4math.net et beaucoup de pratiques. 4math.net Le première clé pour être bon en maths