Olympiade de Mathématiques
( compétition de math destinée aux élèves des lycées et collèges)
Olympiade Math – Géométrie 01 – Exercice 14
voir figure suivante:
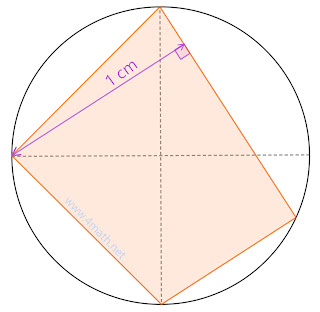
Quadrilatère inscrit dans un cercle,
Calculer sa Surface?
Voir solution
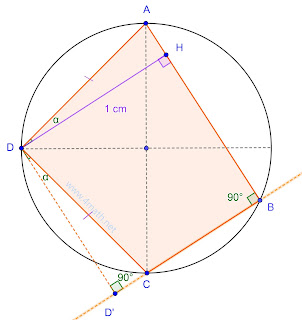
Soit ABCD Quadrilatères inscrits dans le cercle (C) de centre O de rayon R.
Soit D’ la projection de D sur (BC)
* les triangles OAD et ODC sont semblable.
(OA=OD=OC=R et AÔD=DÔC=90°)
➝ AD=DC ①* AĤD=CD̂’D=90° ②
* ABCD Quadrilatères inscrits dans le cercle
somme de deux angles opposés vaut 180°
DÂH+BĈD=180°
* Angle Droite: BĈD+DĈD’=180°
DÂH=DĈD’ ③
①,②&③
les triangles ADHet CDD’ sot équilatéral.
➝ SADH=SCDD’ & DD’=AH=1
* Conclusion:
SABCD=SADH+SHBCD
SABCD=SCDD’+SHBCD
SABCD=SDHBD’ = DHxDD’
(car DHBD’ est un carré)
➡️ SABCD = 1 cm²
Soit ABCD Quadrilatères inscrits dans le cercle (C) de centre O de rayon R.
Soit D’ la projection de D sur (BC)
* les triangles OAD et ODC sont semblable.
(OA=OD=OC=R et AÔD=DÔC=90°)
➝ AD=DC ①* AĤD=CD̂’D=90° ②* ABCD Quadrilatères inscrits dans le cercle
DÂH+BĈD=180°* Angle Droite: BĈD+DĈD’=180°
DÂH=DĈD’ ③
①,②&③
les triangles ADHet CDD’ sot équilatéral.
SADH=SCDD’ & DD’=AH=1
* Conclusion:
SABCD=SADH+SHBCD
SABCD=SCDD’+SHBCD
SABCD=SDHBD’ = DHxDD’
(car DHBD’ est un carré)
➡️ SABCD = 1 cm²
Liens utiles :
Olympiade de Maths, c’est une gymnastique de l’esprit, Ce qu’il faut c’est 4math.net et beaucoup de pratiques
4math.net Le première clé pour être bon en maths