Olympiade Math – Géométrie 01 – Ex 11

Olympiade de Mathématiques
( compétition de math destinée aux élèves des lycées et collèges)


Olympiade Math – Géométrie 01 – Exercice 11


(Puissance d’un point par rapport à un cercle) 
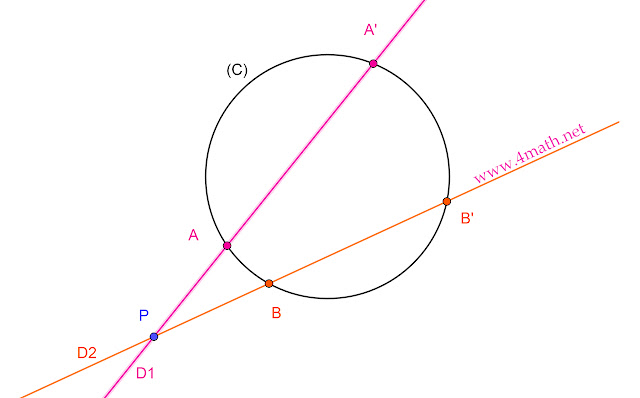
Soit (C) un cercle, 
P un point à l’extérieur de ce cercle. 
(D)droite passant par P et coupant( C) en A et A’  
(D’) droite passant par P et coupant ( C) en B et B’

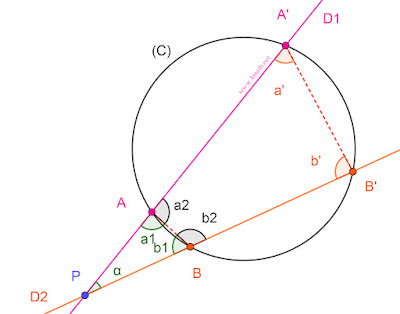
Montrer que PA × PA’ = PB × PB’.

Solution

Montrons que PAB & PB’A’ sont semblables


* on a 
BP̂A=B’P̂A’

* les quartes points ABB’A’ appartenant au même cercle (C) sont dits cocycliques.
➝ Les angles opposés inscriptible sont supplémentaires.
➝ b’+a₂=180° ①

* d’autre part
a₁+a₂=180° ② (PÂA’ angle droite).
① & ②
➡️ b’=a₁ 
l’angle P est le même dans les deux triangles (=α).
➡️  PAB & PB’A’ sont semblables
➝ PA/PB = PB’/PA’
➡️  PA × PA’ = PB × PB’

Liens utiles : 

L’Olympiade Internationale de Mathématiques (OIM)
site officiel de l’OIM, fondation de l’OIM

Olympiade de Maths, c’est une gymnastique de l’esprit, Ce qu’il faut c’est 4math.net et beaucoup de pratiques

4math.net Le première clé pour être bon en maths