Olympiade de Mathématiques
( compétition de math destinée aux élèves des lycées et collèges)
▶️Olympiade Math – Géométrie 01 – Exercice 08
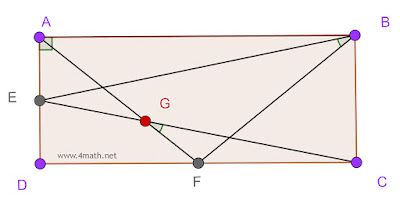
ABCD est un rectangle,
E et F les milieux des côtés [AD] et [DC].
G l’intersection des droites (AF ) et (EC).
Montrer que : les angles CĜF et FB̂E sont égaux.
Solution
ona
*dans le triangle CGF
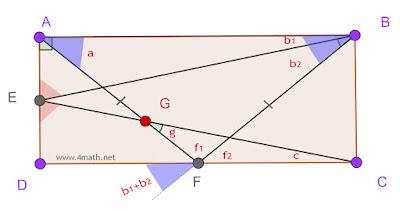
→ CĜF=g=180°-(f₁+f₂+c) ①
Calculons f₁,f₂ et c
* le triangle ABF est isocèle en F(BF=AF)
→ a=b₁+b₂
(somme des angles du triangle ABF)
→ a+b₁+b₂+f₁=180°
→ b₁+b₂+b₁+b₂+f₁=180°
→ f₁=180°-2(b₁+b₂) ②
* ABE & DCE deux triangles semblables
→DĈE=EB̂A
→ c=b₁ ③
* Deux droites parallèles (AB)&(DC)coupées par une sécante (BF)déterminent des angles alternes-internes de même mesure.
→ f₂=b₁+b₂ ④
on remplace ②&③&④ dans ①
① → g=180°-(f₁+f₂+c)
→ g=180°-(180°-2(b₁+b₂)+b₁+b₂+b₁)
→ g=180°-180°+2(b₁+b₂)-b₁-b₂-b₂)
→ g=b₂
▶️ les angles CĜF et FB̂E sont égaux
Liens utiles :
Olympiade de Maths, c’est une gymnastique de l’esprit, Ce qu’il faut c’est 4math.net et beaucoup de pratiques
4math.net Le première clé pour être bon en maths