Olympiade de Mathématique
( compétition de math destinée aux élèves des lycées et collèges)
Des exercices et sujets corrigés pour s’entraîner.
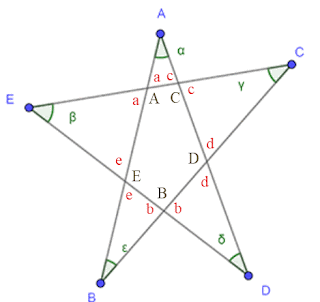
Montrer que:
α+β+γ+ε+δ = 180°
Solution:
☲☲☲
on considère les angles a,b,c,d,e voir figure suivant:
on a
α+a+c=180° (1)
β+a+e=180° (2)
γ+c+d=180° (3)
ε+e+b=180° (4)
δ+b+d=180° (5)
(1)+(2)+(3)+(4)+(5)
⇾ α+β+γ+ε+δ+2(a+b+c+d+e) = 5ｘ180° ①
☲
on considère les angles A,B,C,D,E (Pentagone ABCDE)
ona
A+B+C+D+E=3ｘ180° ②
(=Σ Angles du 3 triangles ABE,CEDet DEB)
☲
d’autre part on a A+a=180°
⇾ A=180°- a ≡ B=180°- b
≡ C=180°- c ≡ D=180°- d ≡ E=180°- e ③
②&③ 180°-a+180°-b+180°-c+180°-d+180°-e=3ｘ180°
a+b+c+d+e= 2ｘ180°
① α+β+γ+ε+δ+2ｘ2ｘ180° = 5ｘ180°
▶️ α+β+γ+ε+δ = 180°
pour les élèves qui aiment
« comprendre », « résoudre » et découvrir de nouvelles façons de raisonner