Olympiade de Mathématique
( compétition de math destinée aux élèves des lycées et collèges)
Des exercices et sujets corrigés pour s’entraîner.
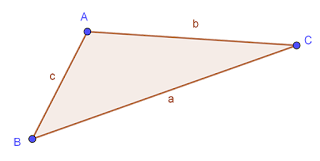
a,b et c trois longueur d’un triangle
Montrer que:
(a+b-c)(b+c-a)(c+a-b) ≤ abc
Solution:
∸∸∸
⊸ a,b et c trois longueur d’un triangle
⇾ a+b>c & b+c>a & c+a>b
⇾ a+b-c>0 & b+c-a>0 & c+a-b>0
⇾ on pose x= a+b-c / y=b+c-a / z=c+a-b
∸∸∸
⊸ on a: x²+y²≥2xy
⇾ (x+y)²≥4xy ①
⇾ (x+y)²≥4xy ①
de même pour
⊸ (y+z)²≥4yz ②
⊸ (z+x)²≥4zx ③
⊸ (y+z)²≥4yz ②
⊸ (z+x)²≥4zx ③
①x②x③ (x,y et z positifs)
⇾ (x+y)² (y+z)² (z+x)² ≥ 4³ x² y² z² ➃
⇾ (x+y)² (y+z)² (z+x)² ≥ 4³ x² y² z² ➃
∸∸∸
on a x= a+b-c & y=b+c-a ⇾ x+y= 2b
➃ ⇾ (2b)² (2c)² (2a)² ≥ 4³ (a+b-c)² (b+c-a)² (c+a-b)²
➃ ⇾ b² c² a² ≥ (a+b-c)² (b+c-a)² (c+a-b)² (a,b et c positifs)
▶️ (a+b-c)(b+c-a)(c+a-b) ≤ abc
pour les élèves qui aiment
« comprendre », « résoudre » et découvrir de nouvelles façons de raisonner