Entraînement
Série 1
Exercice 1
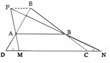
Calculer x dans chacun des cas suivants
Exercice 2
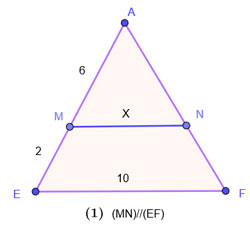
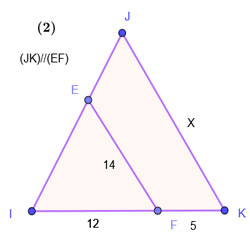
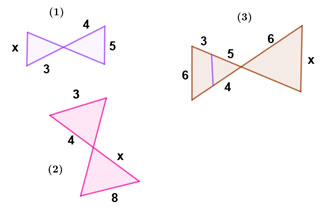
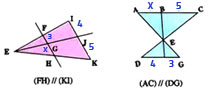
Calculer les valeurs de x dans les figures suivantes
où apparaissent des segments rouges parallèles.
(figures à main levée).
Exercice 3
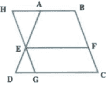
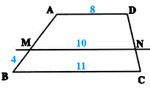
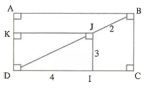
Sur la figure ci-contre:
ABCD est un trapèze ;
(EF)//(DC) ; (HG)//(BC).
AB=5; EF=7
DC = 10 ; CF= 2 et DE =3
Calculer BF et AE .
Exercice 4
On considère la figures ci-contre
Montrer que les droites (FG) et (AB) sont parallèles.
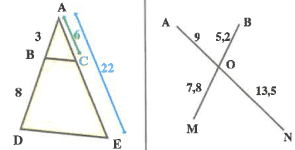
Exercice 5
On considère les deux figures suivantes:
Les droites (BC) et (DE) sont – elles parallèles?
Les droites (AB) et (MN sont- elles parallèles?
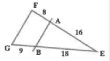
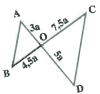
Exercice 6
Sur la figure ci-contre
OA = 3a ; OB = 4,5 a
OC = 7 ,Sa ; OD = 5a
Où a est un nombre positif.
Les droites (AB) et (DC) sont-elles parallèles?
Exercice 7
ADE est un triangle tel que : AE = 3,3 et AD= 2,1
Soit B un point de [ADJ tel que AB = 1,4
et C un point de [AE] tel que : CE= 1,1.
Montrer que : (BC)//(DE).
Série 2
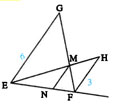
Exercice 8
Sur la figure ci-contre
EM = 8 ; EF = 12 ; EN= 10 NG = 5 et FG = 12.
1) Montrer que (MN)// (FG).
2) Calculer MN.
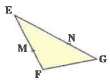
Exercice 9
ABCD est un rectangle de centre O
tel que : AB = 6,3 cm et BC = 4,2 cm.
Soit M un point de [BC] tel que BM =2,8cm et N un point de [BD]
tel que : BN =(frac{1}{3})
Démontrer que : (MN) // (AC).
Exercice 10
Les cercles (C) et (C’) sont concentriques (même centre 0).
En utilisant la réciproque du théorème de Thalès
Démontrer que (AB)//(MN).
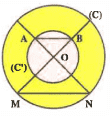
Exercice 11
ABCD est un quadrilatère Soit M un point de [AB].
La parallèle à (BC) passant par M coupe [AC] en N.
La parallèle à (DC) passant par N coupe ADJ en P.
Montrer que les droites (MP) et (DB) sont parallèles.
Exercice 12
Sur la figure ci-contre, (MD)//(NC) et (BC)//(DE)
Démontrer que : (BM)//(NE).
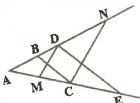
Exercice 13
Calculer TI
sachant que : RA= 1, RT=4, MR = 0,6 et (RM)//(Tl).
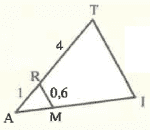
Exercice 14
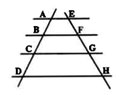
Calculer les valeurs de x dans les figures suivantes :
(où apparaissent des segments parallèles.)
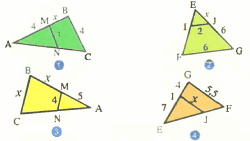
Exercice 15
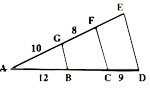
Sur la figure ci-contre: (BG)//(CF)//(DE).
Calculer BC et EF.
Approfondissement
Exercice 1
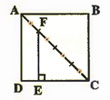
ABCD est un carré de côte 6 cm.
Calculer CE et EF.
Exercice 2
Calculer l’aire et le périmètre du trapèze BCDE
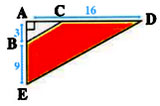
Exercice 3
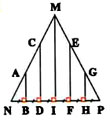
Calculer x dans chacun des cas suivants :
(Figures à main levée).
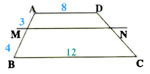
Exercice 4
Sur la figure ci-contre (AE) // (BF) // (CG) // (DH).
Montrer que : (frac{AC}{BD}=frac{EG}{FH})
Exercice 5
Sur la figure ci-contre MNP est un triangle isocèle en M.
MI = 60 et NP = 90.
Calculer AB et CD.
Exercice 6
ABCD est un trapèze bases [AD] et [BC].
Soit M un point de [AB] tel que : AM = 3.
La parallèle à (AD) passant par M coupe [DC] en N.
Calculer MN.
Exercice 7
ABCD est un trapèze tel que (AD)//(BC).
Sur la figure,
on donne : BM=4, AD=8, MN=10 et BC=11
Calculer AM.
Exercice 8
Sur la figure ci-contre, (EG) // (FH) // (NM)
N∊[EF] ;M∊[FG]; M∈[EH] ; EG = 6 ; FH=3.
Calculer MN.
Exercice 9
Reproduire le segment [AB] et construire les points :
1- M de [AB] tel que : (frac{BM}{BA}=frac{5}{7})
2- N de [AB] tel que : (frac{AN}{NB}=frac{5}{7})

Exercice 10
ABCD est un quadrilatère dont les diagonales se coupent en I.
La parallèle à (BC) passant par A coupe (BD) en M.
La parallèle à (AD) passant par B coupe (AC) en N.
Démontrer que : (MN) // (DC).
Devoir
Série 1
Exercice 1
EFGH est un parallélogramme.
Soit A le point de [FG] tel que: GA = (frac{1}{4}) GF.
La parallèle à (FH) passant par A
coupe (GH) en B et (EH) en C.
1)a. Montrer que : (frac{GA}{GF }=frac{AB}{HF}).
b. Montrer que : GA x BC = FA x BA.
2) Soit D un point de [EH] tel que : ED =1/4 EH.
Montrer que : (EG)//(DB).
Exercice 2
EFG est un triangle tel que : EF= 4cm et FG = 5cm.
Soit A un point de [FG] tel que : FA = 3cm.
La parallèle à (EF) passant par A coupe (EG) en B.
1) calculer AB.
2) La parallèle à (AE) passant par F coupe (EG) en C.
La parallèle à (EF) passant par C coupe (FG) en D.
Comparer:
(frac{GA}{GF }=frac{AB}{EF})
puis (frac{GF}{GD}=frac{GE}{GC})
Exercice 3
MARS est un rectangle tels que : MA = 6 et RA= 3.
Soit E un point de (SR) tel que : ER= 3 et E∉[SR].
La droite (ME) coupe (AS) en F et (RA) en H.
1) Calculer HR.
2) Comparer :
(frac{FM}{FE}) et (frac{FA}{FS})
puis (frac{FH}{FM}) et (frac{FA}{FS})
3) Montrer que : FM²= FH x FE.
4) Soit T un point de [MS] tel que : ST = 2.
Montrer que : (TR) // (ME).
Exercice 4
ABC est un triangle tel que :
BC=7 ; AC=5,6 et AB=4,2.
Soit E un point de [AC] tel que : AE= 4.
Exercice 5
La parallèle à (BC) passant par E coupe (AB) en F.
1) Calculer: AF et EF.
2) Soit M un point de [AC) tel que : AM=7,2.
et N un point de [BC) tel que: BN=9.
Montrer que (MN)//(AB).
Série 2
Exercice 5
ABC est un triangle tel que :
AB=15 ; AC=12.
Soit E un point de [AB] tel que : AE = 5.
et F un point de [AC] tel que : AF = 4.
1) Montrer que : (EF) // (BC).
2) La parallèle à (AC) passant par E coupe (BC)
en G ; calculer EG.
Exercice 6
ABCD et AEFH sont des parallélogrammes
Tels que : AB=9, AD=6, E∊[AB],F∊[AC] , H∊[AD]
et (frac{AF}{AC}=frac{1}{3}) ·
1) Calculer AE et AH.
2) Comparer : AE/AB et AH/AD.
3) En déduire que : (EH) // (BD).
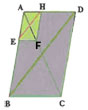
Exercice 7
Sur la figure ci-dessous (EF)//(AC) et (CE)//(BG).
AC=18 ; AB=12 ; AD=10 ; DF=5.
1) Calculer EF et AG.
2) Montrer que : (CF) // (BD).
Exercice 8
EFG est un triangle
Soit M et N deux points à l’extérieur de EFG tels que :
M∊[FE) et N∊[GE).
La parallèle à la droite (MG) passant par N coupe (EF) en A.
La parallèle à (FN) passant par M coupe (EG) en B.
Démontrer que (AB)//(FG).
Exercice 9
l) a. Construire un triangle AST tel que :
AS = 5cm, AT = 7,5cm et ST= 8cm.
b. Placer le point I du segment [SA] tel que: SI= 2cm
c. Tracer la parallèle à la droite (AT) passant par I ;
elle coupe [ST] en J.
2) a. Démontrer que : IJ = 3cm.
b. En déduire la nature du triangle AIJ
ainsi qu’une égalité d’angles.
c. Démontrer que:
la demi-droite [AJ) est la bissectrice de l’angle IÂT
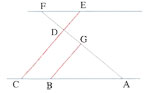
Exercice 10
On considère la figure suivante :
1) Calculer DJ.
2) Calculer l’aire du rectangle ABCD.
Olympiade
Série 1
Exercice 1
ABC est un triangle isocèle en A.
Une droite perpendiculaire à (BC) coupe
respectivement en D, E et F, les droites (BC), (CA) et (AB).
Soit M le milieu de [BC].
1) Montrer que : AE=AF.
2) Démontrer que : (frac{AE}{AB}=2MD)
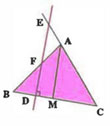
Exercice 2
ABCD est un trapèze de bases [AB] et [DC].
Soit M le point de [BC] tel que : BM =(frac{1}{4})BC.
La parallèle à (DC) passant par M coupe [DB] en N et [AD] en P.
1) Montrer que : DN= (frac{3}{4}) DB.
2) Montrer que : DP= (frac{3}{4}) AD.
3) Montrer que : (DP=frac{3AB+DC}{4})
Exercice 3
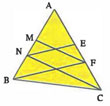
Sur la figure
N∈[AB] , F∈[AC] , (BF)//(NE) et (MF)//(NC)
Montrer que : (frac{AM}{AB}=frac{AE}{AC})
Exercice 4
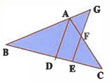
Sur la figure
D est le milieu de [BC] et (EF) // (AD).
Montrer que : EF + EG = 2AD.
Série 2
Exercice 5
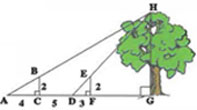
On considère la figure suivante :
1) Calculer GH la hauteur de l’arbre.
2) Calculer AG la distance de A au pied de l’arbre.
Exercice 6
ABC est un triangle. Soit N le milieu de [AC] et M
le point de [AB] tel que : (frac{AM}{AB}=frac{3}{4})
Soit P le point de d’intersection des droites (MN) et
(BC). Démontrer que M est le milieu de [NP].
Exercice 7
ABCD est un parallélogramme.
La bissectrice de l’angle BAD coupe [BD] en E.
La bissectrice de l’angle ABC coupe [AC] en F.
Démontrer que : (EF)//(AB).
Exercice 8
ABCD est un trapèze de bases [AB] et [DC]
tel que : BÂC=90°.
Soit M le milieu de [BD] et N le projeté orthogonal De M sur [AC].
Calculer MN en fonction de AB et DC.
Exercice 9
Soit ABCD un trapèze tel que les droites (AD) et (BC) se coupent en E.
Soit M un point de [DC] et soit N le point de la demi-droite [DC)
tel que : DN>DC et CN= DM
Les droites (AM) et (BM) se coupent en F.
Montrer que : (EF) et (AB) sont parallèles