Exercice 1: (3 Pts)
Thème Analyse :
Partie A:
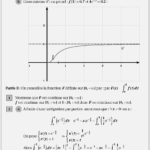
On considère la fonction (f) définie sur ([0,+∞[) par :
si (x>0 ): (f(x)=(1+frac{1}{x}) e^{-frac{1}{x}})
f(0)=0
Soit la courbe de (f) dans un repère orthonormé (( O; vec{ i }, vec{ j }))
(unité graphique : (2 cm) )
1) Montrer que:
(f) est continue et dérivable à droite en (0 .)
2- a) Calculer (lim _{x➝+∞} f(x))
puis interpréter graphiquement le résultat obtenu.
b) Dresser le tableau de variation de (f).
3-a) Montrer que:
(C) admet un point d’inflexion que l’on précisera.
b) Construire (C 😉
en prend (: f(1) approx 0.7) et (4 e ^{-3} approx 0.2)
Partie B :
On considère la fonction (F) définie sur ([0,+∞[) par:
(F(x)=int_{x}^{1} f(t) dt)
1-1) Montrer que:
(F) est continue sur (0 ,+∞[ )
2-a) A l’aide d’une intégration par parties, montrer que ∀x>0:
(int_{x}^{1}(e^{-frac{1}{t}}) dt=e^{-1}-x cdot e^{-frac{1}{x}}-int_{x}^{1}(frac{1}{t} e^{-frac{1}{t}}) dt)
b) Pour (x>0 😉 calculer :
(int_{x}^{1}(1+frac{1}{t}) e ^{-frac{1}{t}} d t).
Puis montrer que:
(lim _{x ➝ 0^{+}}int_{x}^{1} f(x) d x=frac{1}{e}).
3) On considère la suite ((u_{n})) définie sur (N) par:
(u_{n}=F(n)-F(n+2))
a) En utilisant le théorème des accroissements finis,
montrer que :
((∀n∈ N )(∃ v_{n}∈] n, n+2[), u_{n}=2(1+frac{1}{v_{n}}) e ^{-frac{1}{v_{n}}})
b) Montrer que (∀n∈IN ^{*} ):
(2(1+frac{1}{n}) e ^{-frac{1}{n}}<u_{n}<2(1+frac{1}{n+2}) e ^{-frac{1}{n+2}}).
En déduire (lim _{n ➝+∞} u_{n}).
Partie C:
1-a) Montrer que:
((∀n∈IN ^{*})(∃! α_{n}>0), f(α_{n})= e ^{-frac{1}{n}})
b) Montrer que la suite ((α_{n})) est croissante.
c) Justifier que (∀n∈IN ^{*} ) on a :
(-frac{1}{α_{n}}+ln (1+frac{1}{α_{n}})=-frac{1}{n})
2-a) Montrer que (∀ t geq 0,1-t≤ frac{1}{1+t}≤ 1-t+t^{2})
b) En déduire que:
((∀x geq 0),-frac{x^{2}}{2}≤ -x+ln (1+x)≤ -frac{x^{2}}{2}+frac{x^{3}}{3})
3) Soit (n) un entier tel que (n geq 4)
a) Vérifier que (α_{4} geq 1)
puis déduire que (α_{n} geq 1)
sachant que (e ^{frac{3}{4}} geq 2)
b) Montrer que :
(1-frac{2}{3 α_{n}}≤ frac{2 α_{n}^{2}}{n}≤ 1 .)
(On peut utiliser : (1-c) et (2-b) partie C:
c) Montrer que : (sqrt{frac{n}{6}}≤ α_{n} .)
En déduire (lim _{n ➝+∞} α_{n})
d) Calculer:
(lim _{n ➝+∞}(α_{n} sqrt{frac{2}{n}}))
Exercice 2: (3 Pts)
Thème Arithmétiques:
Les parties A et B sont indépendantes
Partie A :
Afin de crypter un message, on utilise un chiffrement affine Chaque lettre de l’alphabet est associée à un nombre entier comme indiqué dans le tableau ci-dessous:
Soit (x) le nombre associé à la lettre à coder.
On détermine le reste (y) de la division euclidienne de (7 x+5) par 26 ,
puis on en déduit la lettre associée à (y)
(c’est elle qui code la lettre d’origine).
Exemple : M correspond à (x=12 .)
On a (7×12+5=89)
Or (89 ≡ 11[26]) et 11 correspond à la lettre (L_{2})
donc la lettre M est codée par la lettre L.
1) Coder la lettre L.
2-a) Soit (k) un entier relatif.
Montrer que si (k ≡ 7 x[26]) alors (15 k ≡ x[26]).
b) Démontrer la réciproque de l’implication précédente.
c) En déduire que (y ≡ 7 x+5) [26] équivaut à (x ≡ 15 y+3[26]).
3) À l’aide de la question précédente décoder la lettre (F).
Partie B :
On considère les suites ((a_{n})) et ((b_{n})) telles que:
(a_{0}) et (b_{0}) sont des entiers compris entre 0 et 25 inclus
et pour tout entier naturel:
(n, a_{n+1}=7 a_{n}+5) et (b_{n+1}=15 b_{n}+3).
Montrer que pour tout entier naturel (n):
(a _{n}=(a_{0}+frac{5}{6})×7^{n}-frac{5}{6}).
On admet pour la suite du problème que:
((∀n∈ N ), b_{n}=(b_{0}+frac{3}{14})×15^{n}-frac{3}{14}).
Exercice 3: (3 Pts)
Thème Nombres complexes:
On considère les nombres complexes (z_{n}) définis, pour tout entier naturel (n), par:
(z_{0}=1) et (z_{n+1}=(1+ i frac{sqrt{3}}{3}) z_{n})
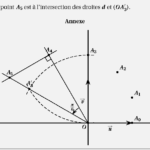
On note (A_{n}) le point d’affixe (z_{n}) dans le repère orthonormé
(( O ; vec{ u }, vec{ v })) de l’annexe.
L’objet de cet exercice est d’étudier la construction des points (A_{n})
1-a) Vérifier que:
(1+ i frac{sqrt{3}}{3}=frac{2}{sqrt{3}} e ^{ i frac{pi}{6}}).
b) En déduire:
(z_{1}) et (z_{2}) sous forme exponentielle.
2-a) Montrer que pour tout entier naturel n:
(z_{n}=(frac{2}{sqrt{3}})^{n} e ^{ i n frac{pi}{6}}).
b) Pour quelles valeurs de (n), les points (O , A_{0}) et (A_{n}) sont-ils alignés?
3) Pour tout entier naturel (n), on pose (d _{ n }=|z_{n+1}-z_{n}|).
a) Interpréter géométriquement (d_{n}).
b) Calculer (d_{0}).
c) Montrer que ∀n∈ IN ^{*}:
(z_{n+2}-z_{n+1}=(1+ i frac{sqrt{3}}{3})(z_{n+1}-z_{n})).
d) En déduire que la suite ((d_{n})_{n geqslant 0}) est géométrique
puis que ∀n∈ IN : (d_{n}=frac{sqrt{3}}{3}(frac{2}{sqrt{3}})^{n})
4-a) Montrer que pour tout entier naturel n:
(|z_{n+1}|^{2}=|z_{n}|^{2}+d_{n}^{2}).
b) En déduire que pour tout entier naturel n:
le triangle (OA_{n}A_{n+1}) est rectangle en (A_{n}).
c) Construire, à la règle non graduée et au compas, le point (A_{5})
sur la figure de l’annexe.
d) Justifier cette construction.
➲ Si vous souhaitez signaler une erreur merci de nous envoyer un commentaire
Correction Examen National Math 2 Bac Science Math 2021 Bac Blan 2 Correction :