Olympiade de Mathématiques
( compétition de mathématiques destinée aux élèves des lycées et collèges)
Des exercices et sujets corrigés pour s’entraîner.
Des exercices et sujets corrigés pour s’entraîner.
Olympiade de Mathématiques – Géométrie Niveaux 01 – Exercice 04
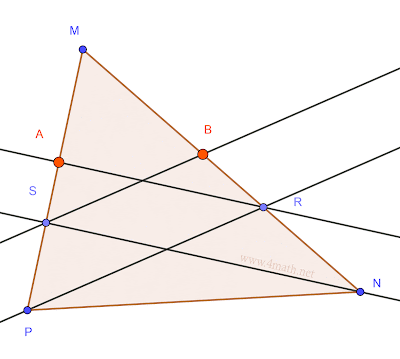
Soit MNP un triangle, R,S,A et B quatre points tel que:
R∊[MN], S∊[MP], (PR)//(BS)et (AR)//(NS)
Dans le triangle MSN ona (AR)//(SN)
D’après le théorème de Thalès, on a : MA/MS = MR/MN
⇾ MAxMN = MRxMS ①
Dans le triangle MRP ona (SB)//(PR)
D’après le théorème de Thalès, on a : MB/MR = MS/MP
⇾ MBxMP = MRxMS ②
①&② ⇾ MAxMN = MBxMP
Donc:
MA/MP = MB / MN
pour les élevés qui aiment
« comprendre », « résoudre » et découvrir de nouvelles façons de raisonner