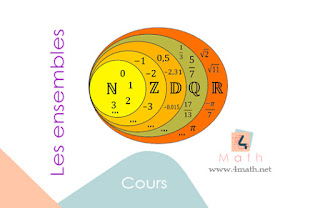
1- Différents types de nombres
1- Nombres entiers naturels IN
( N est le premier lettre du mot naturels)
Exemple: 0;1;2;3;…
N* (N étoile) est l’ensemble des entiers naturels sauf 0 (zéro)
( Z est le premier lettre du mot Zahl = nombre).
L’ensemble Z contient les nombres naturel positive & negative
Exemple:…-3;-2;-1;0;1;2;3….
on dit que (-5) appartient à l’ensemble Z, et on écrit: (-5)∈Z
L’ensemble N est inclus dans l’ensemble Z ( IN⊂Z)
* ID est représentés par a x 10ⁿ, où a et n sont des éléments de Z.
* l’ensemble des nombres décimaux ID sont des nombres qui peuvent s’écrire avec un nombre fini de chiffres.
Exemple: -12.55 │ -2.1 │ -1 │ 0 │ 9 │ 3.7 │ 7.8434
Q est représenté par une fraction a/b avec a∈Z et b∈Z*
Exemple: 1/7 │ -3/2 │ 5/22 │ 1/1234
R est l’ensemble de tous les nombres qui peuvent exister réellement, il contient en plus des nombres rationnels, les nombres non rationnels ou irrationnels comme racine carré de 2 et π.
IN C Z C ID C Q C IR
2- Identités remarquables
* Identité remarquable Second degré
Pour tous réels a et b, on a :
Il y a 3 formules, à connaître par cœur :
pour développer:
Carré d’une somme : (a + b)² = a² + 2ab + b²
Carré d’une différence : (a – b)² = a² – 2ab + b²
Différence de deux carrés : (a + b) (a – b)=a² – b²
a² + 2ab + b²=(a + b)²
a² – 2ab + b²=(a – b)²
a² – b² =(a + b) (a – b)
développer:
(2x + 3)² = 4x² + 12 x + 9
(x+3)(x-3)=x²-9
9x² – 30x + 25=(3x-5)²
4x²-49=(2x-7)(2x+7)
* Identité remarquable 3éme degré
(a + b)³ = a³ + 3a² b + 3ab² + b³
3- Ecriture scientifique
Les scientifiques doivent souvent écrire de très grands ou de très petits nombres. Ils ont alors recours à une notation particulière appelée notation scientifique.
Les nombres sont écrits, en notation scientifique, sous la forme générale :
a.10p ou a∈ ID 1≤ a <10 / p ∈ Z
« 123 000 000 000 000 est beaucoup moins parlant que 1,23 x 10¹⁴ »
Exemples: 5 x 10⁶ │ 7.2x 10⁻³ │ -5,06 x 10¹⁵
Ces nombres ne sont pas écrits en notation scientifique :
0.5 x10⁻³ │ 16 x 10¹¹
Astuce pour écrire un nombre sous forme scientifique:
0.5 x 10⁻³ = 5×10⁻⁴ │ 16 x 10¹¹ = 1.6 x 10¹² │ 10⁶ = 1 x 10⁶