Résumé Cours Etudes de fonctions
* Domaine de définition
l’ensemble de définition de f c’est l’ensemble des nombres x tels que leur image f (x) existe.
On peut le noter D f.
4 types d’expressions posent problème :
1èr cas: L’expression de f (x) est de la forme:
\(f(x)=\frac{g(x)}{h(x)}\)est définie lorsque h(x)≠0.
(on ne peut pas diviser par zéro)
Exemple:
\(f(x)=\frac{x}{x²-4}+\frac{1}{x+1}\)
x ∈ Df ⟶ x²-4 ≠0 et x+1 ≠0 ➝ Résoudre d’équation: x²-4=0 et x+1=0
D f = IR-{-2;-1;2}.
2ème cas: L’expression de f (x) est de la forme:
\(f(x)=\sqrt{g(x)}\)est définie lorsque g(x)⩾0.
(la racine carrée n’existe que pour des nombres positifs ou nuls)
Exemple:
\(f(x)=x-2 \sqrt{x²-1}+2\)
x ∈ Df ⟶ x²-1 ≥ 0 ➝ Table de variation : Df =]-∞,-1]∪[1,+∞[.
3ème cas: L’expression de f (x) est de la forme:
\(f(x)=\frac{g(x)}{\sqrt{h(x)}}\)est définie lorsque \(h(x)>0\).
(c’est une combinaison des 2 cas précédents…)
Exemple:
Exemple:
\(f(x)=\frac {x²}{2\sqrt{x-3}}+2x+1\)
x ∈ Df ⟶ x-3 > 0 ➝ Table de variation : Df =]3,+∞[.
4ème cas: L’expression de f (x) est de la forme:
f(x)=log(g(x)) est définie lorsque g(x)>0.
(les expressions qui se trouvent à l’intérieur des logarithmes sont strictement positives).
Exemple:
f(x)=ln(x²-3x+2)
x ∈ Df ➝ x²-3x+2 > 0 ➝ Table de variation : Df =]-∞,1[∪]2,+∞[.
Dans les autres cas étudiés les fonctions sont en général définies sur R, c’est à dire qu’on peut calculer l’image de n’importe quel nombre réel.
Astuce:
\(f(x)=\left\{\begin{array}{ll} f_{1}(x) & , x∊I \\ f_{2}(x) & , x∊J \end{array}\right.\)
\(Df = ( Df_{1}∩I ) ∪ ( Df_{2}∩I )\).
Exemple:
\(f(x)=\left\{\begin{array}{ll} x-\frac{3}{2}+\frac{2x+1}{ x²-1} & , x∊]-∞,0] \\ 1+(\frac{\ln (x-1)}{x²+1})^{2} & , x∊]0,+∞[ \end{array}\right.\)
Calculer Df ?
* Df₁:x∊]-∞,0]
x∊Df₁ ⟶ x²-1≠0 ⟶ x≠1 et x≠-1 et x∊]-∞,0]
⟶ Df₁ =]-∞,-1[∪]-1,0]
* Df₂: x∊]0,+∞[
x∊Df₂ ⟶ x-1>0 et x²+1≠0 (vraie) ⟶ x>1 et x∊]0,+∞[
⟶ Df₂ =]1,+∞[
Df = Df₁ ∪ Df₂ = ]-∞,-1[∪]-1,0]∪]1,+∞[.
* Fonction continue
* Continuité sur un intervalle
une fonction définie sur un intervalle I est continue sur I
⟶ on peut tracer sa courbe représentative sans lever le crayon.
Exemple:
* Les fonctions : polynômes, exponentielle continues sur IR .
* Les fonctions rationnelles sont continues sur chaque intervalle contenu dans leur ensemble de définition.
* La fonction racine carrée est continue sur IR+.
* La fonction logarithme est continue sur IR+*.
* Continuité en un point
Soit \(f\) une fonction numérique définie sur un intervalle ouvert ouvert I et x₀∈I.
f est continue en x₀ ⇔ \(\lim _{x \rightarrow { x_{0}}} f(x)=f\left(x_{0}\right)\).
Exemple:
\(f(x)=\left\{\begin{array}{ll}\ln \left(1-x^{3}\right) ; & x<0 \\ 4 x \sqrt{x}-3 x^{2} ; & x \geq 0\end{array}\right.\)
Continuité en 0 ?
on a:
* \(f(0)=4 \times 0 \times \sqrt{0}-3 \times 0^{2}=0\)
* \(\lim _{x \rightarrow 0^{+}} f(x)\)
\(=\lim _{x \rightarrow 0^{+}} 4 x \sqrt{x}-3 x^{2}\)
=0=f(0).
⟶ f est continue droite en 0
* \(\lim _{x \rightarrow 0^{-}} f(x)\)
\(=\lim _{x \rightarrow 0^{-}} \ln \left(1-x^{3}\right))\)
=0=f(0).
⟶ f est continue gauche en 0
Donc:
\(\lim _{x \rightarrow 0^{+}} f(x)=\lim _{x \rightarrow 0^{-}}f(x)=f(0)\)
⟶ f est continue en 0.
* Dérivabilité et interprétation graphique
* Dérivabilité:
-Soit f une fonction numérique définie sur un intervalle ouvert I et x₀∈I.
* f est dérivable en x₀, s’il existe un nombre réel \(l\) tel que:
\(\lim _{x⟶x₀} \frac{f(x)-f(x₀)}{x-x₀}=l=f^{\prime}(x₀)\).
* Interprétation graphique:
L’équation de la tangente T à \(C_{f}\) en point d’abscisse x₀ est :
\(y=f^{\prime}(x₀)(x-x₀ )+f(x₀)\).
* f est dérivable à droite au point d’abscisse x₀ s’il existe un réel \(l\) tel que:
\(\lim _{x⟶x₀⁺} \frac{f(x)-f(x₀)}{x-x₀}=l=f_{d}^{\prime}(x₀)\).
* Interprétation graphique:
L’équation de la tangente T à \(C_{f}\) à droite au point d’abscisse x₀ est :
\(y=f_{d}^{\prime}(x₀)(x-x₀ )+f(x₀)\).
* f est dérivable à gauche au point d’abscisse x₀ s’il existe un réel \(l\) tel que:
\(\lim _{x⟶x₀⁻} \frac{f(x)-f(x₀)}{x-x₀}=l=f_{g}^{\prime}(x₀)\).
* Interprétation graphique:
L’équation de la tangente T à \(C_{f}\) à gauche au point d’abscisse x₀ est :
\(y=y=f_{g}^{\prime}(x₀)(x-x₀ )+f(x₀)\).
** \(f_{d}^{\prime}(x₀)=f_{g}^{\prime}(x₀)\) ⇔ f est dérivable en x₀
Exemple:
\(f(x)=x-2 \sqrt{x}+2\) dérivabilité en 0⁺ ?
On a:
\(\lim _{x⟶0⁺} \frac{f(x)-f(0)}{x-0}\)
\(=\lim _{x⟶0⁺} \frac{x-2 \sqrt{x}+2-2}{x}\)
\(=\lim _{x⟶0⁺} \frac{x (1-\frac{2}{\sqrt{x}})}{x}\)
\(=\lim _{x⟶0⁺} 1-\frac{2}{\sqrt{x}}\)
=1-(+∞)= -∞ ∉ IR ( car \(lim _{x⟶0⁺}\sqrt{x}=+∞\)).
⟶ f n’est pas dérivable en 0⁺.
| Fonction |
Dérivée |
D f ‘ |
| k (k∈R) |
0 |
IR |
| x |
1 |
IR |
| \(x^{n}\) (n∈N) |
\(n x^{n-1}\) |
IR |
| \(\frac{1}{x^{n}}\) (n∈N) |
\(-\frac{n}{x^{n+1}}\) |
R−{0} |
| \(\sqrt{x}\) |
\(\frac{1}{2\sqrt{x}}\) |
]0;+∞[ |
| sin(x) |
cos(x) |
IR |
| cos(x) |
−sin(x) |
IR |
| \(e^{x}\) |
\(e^{x}\) |
IR |
| ln(x) |
\(\frac{1}{x}\) |
]0;+∞[ |
* Opérations sur les fonctions dérivables
Soit u une fonction dérivable sur intervalle I et v une fonction dérivable sur intervalle J.
* \((u+v)’=u’+v’\).
* \((u×v)’=u’×v + u×v’\).
* \((\frac{u}{v})’\)=\(\frac{u’×v – u×v’}{v²}\).
* Théorème de la dérivée des fonctions composées
Soit g une fonction dérivable sur un intervalle I et prenant ses valeurs dans un intervalle J et soit f une fonction dérivable sur J : (f(g(x)) ‘ = g ‘ (x) × f ‘ (g(x).
Application:
Soit u une fonction dérivable sur intervalle I :
* la fonction \(u^{n}\) est dérivable sur I et sa dérivée est \(u^{\prime}\times nu^{n-1}\).
* la fonction \(\frac{1}{u}\) est dérivable sur la partie de I où u≠0 et sa dérivée est \(-\frac{u^{\prime}}{u^{2}}\).
* la fonction \(\sqrt{u}\) est dérivable sur la partie de II où u > 0 et sa dérivée est \(\frac{u^{\prime}}{2\sqrt{u}}\).
* la fonction \(\sin(u)\) est dérivable sur I et sa dérivée est \(u^{\prime}\times \cos(u)\).
* la fonction \(\cos(u)\) est dérivable sur I et sa dérivée est \(-u^{\prime}\times \sin\left(u\right)\).
* la fonction \(e^{u}\) est dérivable sur I et sa dérivée est \(u^{\prime}\times e^{u}\).
* la fonction \(\ln(u)\) est dérivable sur la partie de I où u>0 et sa dérivée est \(\frac{u^{\prime}}{u}\).
Exemple:
((5x+2)³)’ = 3(5x+2)’(5x+2)³⁻¹ = 3×5(5x+2)² = 15(5x+2)².
sin(2x+2)‘=(2x+2)’sin'(2x+2)=2cos(2x+1).
(\(\frac{ln(x)}{x²+1})\))’=\(\frac{ln(x)’×(x²+1) – ln(x)×(x²+1)’}{(x²+1)²}\)
=\(\frac{\frac{1}{x}×(x²+1) – ln(x)×(2x)}{(x²+1)²}\)
=\(\frac{\frac{x²+1}{x} – ln(x)×(2x²)}{(x²+1)²}\)
=\(\frac{x² + 1 – 2x²ln(x)}{x(x²+1)²}\).
* Extremums
Soient f une fonction dérivable sur un intervalle I et x₀ ∈ I.
* Si f ‘ s’annule et change de signe en x₀, alors f admet un extremum en x
et \(C_{f}\) admet une tangente horizontale au point d’abscisse x₀.
Exemple :
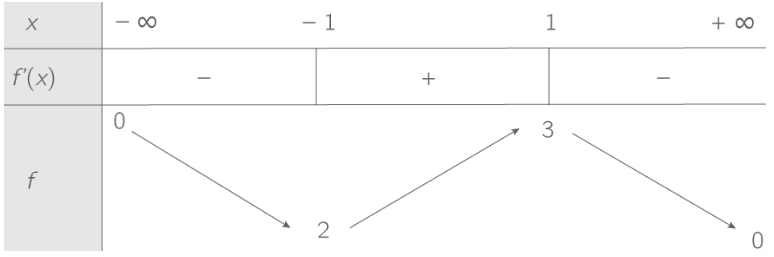
* Le minimum de f est 2 atteint pour x=-1.
* Le maximum de f est 3 atteint pour x=1.
Exemple :

* Le minimum de f est atteint pour x=1.
* Le maximum de f est atteint pour x=3.
Non dérivabilité en un point :
Soit f une fonction numérique définie sur un intervalle ouvert I et x₀∈I.
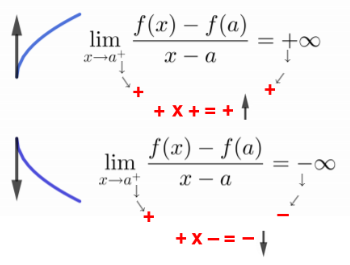
si on a: \(\lim _{x⟶x₀^{±}} \frac{f(x)-f(x₀)}{x-x₀}=±∞\)
⟶ f n’est pas dérivable en x₀ et \(C_{f}\) admet une demi-tangenteverticale (T) à droite ou à gauche du point d’abscisse x₀.

* Point d’inflexion
* si f » s’annule et change de signe en a alors le point A (a;f(a)) est un point d’inflexion de \(C_{f}\).
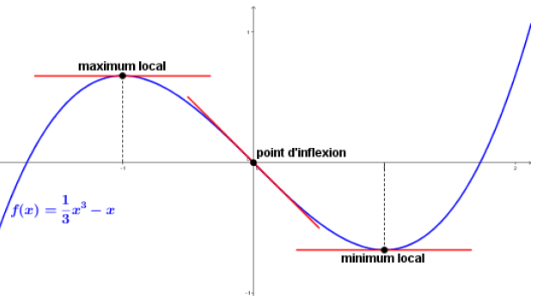
* si f ‘ s’annule et ne change pas de signe en a alors le point \(A (a;f(a))\) est un point d’inflexion de \(C_{f}\).

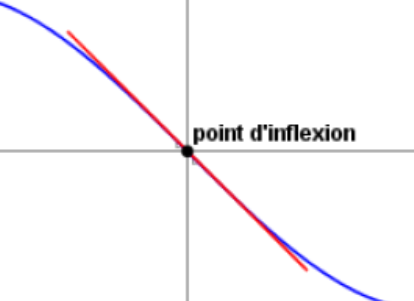
* Asymptotes
* Limite finie quand x tend vers l’infini:
\(\lim _{x⟶±∞}f(x)=b\)
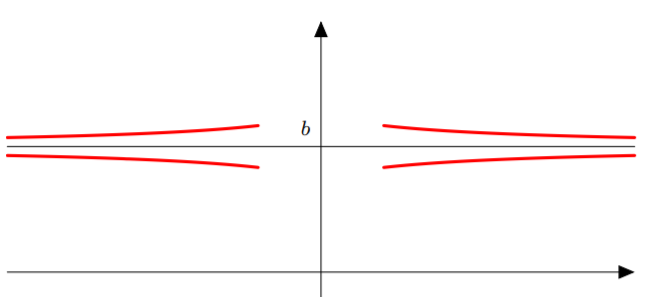
⟶ \(C_{f}\) admet une asymptote horizontale d’équation y = b au voisinage de +∞ ou x = −∞.
* Limite infinie quand x tend vers un réel:
\(\lim _{x⟶ a}f(x)=±∞\)
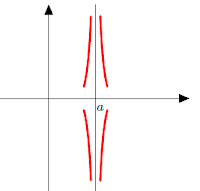
⟶ \(C_{f}\) admet une asymptote verticale d’équation x = a à droite ou à gauche du point d’abscisse a.
* Limite infinie quand x tend vers l’infini:
\(\lim _{x⟶ ±∞}f(x)=±∞\)
1èr cas: \(\lim _{x⟶±∞} \frac{f(x)}{x}=±∞\)
\(C_{f}\) admet une branche parabolique suivant (oy) au voisinage de ±∞.
2èr cas: \(\lim _{x⟶±∞} \frac{f(x)}{x}=0\)
\(C_{f}\) admet une branche parabolique suivant (ox) au voisinage de ±∞.
3èr cas: \(\lim _{x⟶±∞} \frac{f(x)}{x}=a\)
\(\lim _{x⟶±∞} f(x)-ax.\) =\(\left\{\begin{array}{ll} b : ① \\ ±∞ : ② \end{array}\right.\)
①: la droite y = ax + b est une asymptote oblique à \(C_{f}\) au voisinage de ±∞.
②: \(C_{f}\) admet une branche parabolique suivant (D) : y = ax au voisinage de ±∞.
* y = ax + b est une asymptote oblique:
La droite d’équation y = ax + b est une asymptote oblique à \(C_{f}\) au voisinage de ±∞
⇔ \(\lim _{x⟶ ±∞}f(x)-(ax + b)=0\)
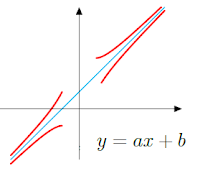
* Positon relative d’une courbe et une droite
Pour étudier la positon relative d’une courbe \(C_{f}\) et une droite (D) d’équation y = ax +b:
→ étudie le signe de la différence : f ( x) − y.
* l’intersection avec les axes du repère
* avec l’axe des ordonnées (oy): on est à l’abscisse 0,
donc on cherche l’image de 0 par la fonction. f(0)=…
⟶ \(C_{f}\) ∩(oy) = {A(0; f (0))}.
* avec l’axe des abscisses (ox): on est l’ordonnée 0, donc on cherche les antécédents de 0,
cela revient à chercher les valeurs de x, tels que f(x)=0:
(on suppose que x₁;x₂… solution de f(x)=0)
⟶ \(C_{f}\) ∩ (oy) = {A(x₁; f (x₁);A(x₂; f (x₂);….}.
* Théorème des valeurs intermédiaires
* Fonction continue:
Si f est une fonction continue sur un intervalle [a;b] et si k est compris entre f(a) et f(b),
alors l’équation f(x)= k au moins une solutionc sur l’intervalle [a;b] (f(c)=k).
* Fonction continue et strictement monotone:
Si f est une fonction continue sur un intervalle [a;b] et si k est compris entre f(a) et f(b),
alors l’équation f(x)= k admet une unique solution c sur l’intervalle [a;b] (f(c)=k).
Exemple:
Montrer que l’équation : f(x)=0 admet une unique solution unique sur l’intervalle [2.6 ; 6]
On a: la fonction f continue et strictement monotone sur [2.6 ; 6] (table de variation).
et on a: f(2.6)=3.5 et f(6)=-9.
On en déduit, d’après le théorème des valeurs intermédiaires pour tout réel k compris entre 3.5 et -9,
l’équation f(x)=k admet une unique solution c dans [2.6 ; 6].
Soit k=0: L’équation s’écrit f(x)=0.
D’après le théorème précédent, cette équation admet une unique solution c dans [2.6 ; 6].
Exemple:
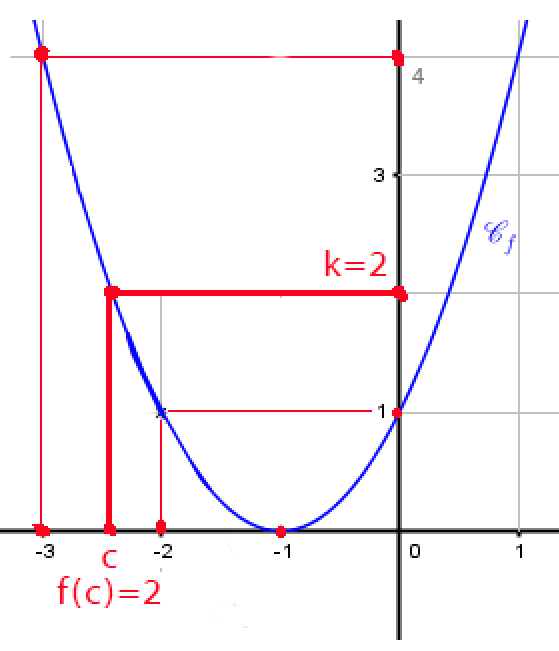
Montrer que l’équation : f(x)=2 admet une unique solution unique sur l’intervalle [-3 ; -2]
On a: la fonction f continue et strictement monotone sur [-3 ; -2] (la courbe de \(C_{f}\)).
et on a: f(-3)=4 et f(-2)=1.
d’après le théorème des valeurs intermédiaires pour tout réel k compris entre -4 et 1,
l’équation f(x)=k admet une unique solution c dans [-3 ; -2].
Soit k=2: l’équation f(x)=2 admet une unique solution c dans [-3 ; -2].
* La fonction réciproque
f est une fonction continue et strictement monotone sur un intervalle I
J= f(I) est un intervalle de même nature que I (fermé, ouvert ou semi ouvert) et ses extrémités sont les limites de f aux extrémités de I.
⟶La fonction f admet une fonction réciproque définie sur J=f(I) noté f ⁻¹ de J ver I.
1) Calcule de f⁻¹(x):
y= f(x) (x∊I) ⇔ x=f⁻¹(y) (y∊J).
Exemple:
f(x)=x²-1 avec x∊I=[2,3]
on a f continue et strictement croissante sur un intervalle I=[2,3].
et J=J= f(I) =[f(2),(3)]=[3,8].
Alors f admet une fonction réciproque définie sur [3,8] par:
x∊I=[2,3] et y∊I=[3,8]
y=f(x)=x²-1 ⟶ x= \(\sqrt{y+1}\)
donc: f⁻¹(x)= \(\sqrt{x+1}\) avec x∊I=[3,8] (on change x avec y)
2) Continuité de f ⁻¹: f ⁻¹ est continue sur J=f (I).
3) Monotonie de f ⁻¹: f ⁻¹ est strictement monotone sur J=f (I)
de même sens de monotonie que de f sur I.
4) Courbe de \(C_{f⁻¹}\): la Courbe \(C_{f ⁻¹}\) est symétrique la courbe \(C_{f}\)
par rapport à la droite d’équation : y = x.
* L’axe de symétrie
La droite d’équation x = a est l’axe de symétrie de la courbe \(C_{f}\).
⇔ ∀∊\(D_{f}\): (2a − x)∊\(D_{f}\) et f(2a − x) = f (x).
Exemple: f(x)=x²-2x Montrer que: x=1 est l’axe de symétrie de la courbe \(C_{f}\).
on a : a=1 et \(D_{f}\)=IR
* ∀ x∊IR : (2 − x)∊IR (2a-x=2-x)
* f(2a-x)=(2-x)²-2(2-x)=4-4x+x²-4x+2x=x²-2x=f(x).
⟶ x=1 est l’axe de symétrie de la courbe \(C_{f}\).
* Le centre de symétrie
Le point A(a;b) est le centre de symétrie de la courbe \(C_{f}\).
⇔ ∀ x∊\(D_{f}\) : (2a − x)∊\(D_{f}\) et f (2a − x) = 2b − f (x).
Exemple: \(f(x)=\frac{x-1}{x-2}\)Montrer que: A(2,1) est le centre de symétrie de la courbe \(C_{f}\).
on a : a=2 , b=1 et \(D_{f}\)=IR-{2}
(2a-x)=2 ↔️ 4-x=2↔️ x=2
d’où: ∀x∊IR-{2}: (2 − x)∊IR-{2}
d’autre part:
* f(2a-x)=f(4-x)=(\(\frac{(4-x)-1}{(4-x)-2})\)=(\\frac{3-x}{2-x}\)
* 2b-f(x)=2-f(x)=(\2-\frac{x-1}{x-2}\)=\frac{2x-4-x+1}{x-2}\)=\frac{3-x}{2-x})\)
donc: f(2a-x)=2b-f(x)
⟶ x=1 est l’axe de symétrie de la courbe \(C_{f}\).
Résumé du Cours pour Bac 2


