Bac Economie et Gestion Session Principale 2019 Pdf
Avec Correction
Avec Correction
Durée de l’épreuve 2h
L’épreuve est composée de trois exercices et un problème
indépendants entre eux et répartis suivant les domaines comme suit:
* Calcule Matriciel (4.5 points )
* Calcule Matriciel (4.5 points )
* Statistique (4.5 points )
* Etude d’une fonction numérique (6 points )
* Suite Numérique (5 points )
* Calcule Matriciel (4.5 points )
\(A=\left(\begin{array}{ccc}4 & -2 & 6 \\ 3 & -1 & 5 \\ -1 & 1 & -3\end{array}\right), B=\left(\begin{array}{ccc}3 & 0 & 2 \\ -2 & 5 & 1 \\ -1 & 1 & 1\end{array}\right)\)
On donne les matrices et \(I_{3}=\left(\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right)\)
1) a) Calculer le déterminant de \(A\) et déduire que la matrice A est inversible
b) Calculer la matrice \(A×(B-2 I_{3})\)
puis déduire la matrice inverse de \(A\).
2) Soit dans\(R ^{3}\) le système \(( S ):\)
\(\left\{\begin{array}{l}4 x-2 y+6 z=1 \\ 3 x-y+5 z=2 \\ -x+y-3 z=1\end{array}\right.\)
a) Existe-t-il un réel \(α\) pour que le triplet \((α, α, 0)\) soit une solution de (S) Justifier votre réponse
b) Montrer que :\((a, b, c)\) est solution de:
(S) si et seulement \(si \left(\begin{array}{l} a \\ b \\ c \end{array}\right)=\left(\begin{array}{ccc}\frac{1}{2} & 0 & 1 \\ -1 & \frac{3}{2} & \frac{1}{2} \\ -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2}\end{array}\right)\left(\begin{array}{l}1 \\ 2 \\ 1\end{array}\right)\)
c) Résoudre alors dans \(R³\) le système \(( S )\).
* Statistique (4.5 points )
Dans le tableau suivant on donne l’évolution du prix moyen (en millimes)
d’un litre d’essence sans plomb entre les années 2009 et 2017
\(\begin{array}{|l|c|c|c|c|c|c|c|c|c|}\hline année & 2009 & 2010 & 2011 & 2012 & 2013 & 2014 & 2015 & 2016 & 2017 \\\hline Rang\; de\; l’année\; x _{ i } & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\\hline Prix\; moyen\; y _{ i } & 1270 & 1320 & 1370 & 1420 & 1490 & 1570 & 1640 & 1670 & 1750 \\\hline\end{array}\)
1) a) Représenter le nuage de points de la série statistique \(\left(x_{i} ; y_{i}\right)\) dans l’annexe ci-jointe.
b) Justifier que ce nuage permet d’envisager un ajustement affine.
c) Calculer les coordonnées du point moyen G de ce nuage et le placer.
2) a) Déterminer par la méthode des moindres carrées
une équation cartésienne de la droite de régression D de y en x.
b) Tracer la droite D.
c) En utilisant cet ajustement,
estimer le prix moyen d’un litre d’essence sans plomb pour l’année 2023
* Etude d’une fonction numérique (6 points )
Soit la fonction \(f \)définie sur ]0,+∞[ par:
f(x)=(x-1)lnx et \(C\) sa courbe représentative dans un repère orthonormé
\((O,\vec{i},\vec{j})\)
1) a) Calculer \(\lim _{x➝0^{-}} f(x)\) puis interpréter graphiquement le résultat obtenu.
b) calculer \(\lim _{x➝+∞} f(x)\) puis vérifier que \(\lim _{x➝+∞} \frac{f(x)}{x}=+∞\)
et interpreter graphiquement ce résultat.
2) Justifier que \(f \) est dérivable sur }]0,+∞[
et que \(f ‘(x)=ln x+\frac{x-1}{x}\) pour tout x∈]0,+∞[
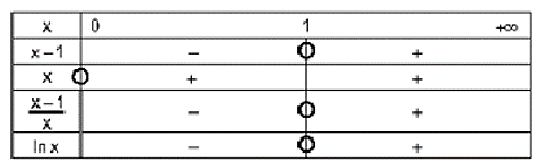
3) a) Montrer que : \(lnx\) et \(\frac{x-1}{x}\) sont de même signe
sur chacun des intervalles }]0,1[ ct ] 1,+∞[
b) Dresser alors le tableau de variations de \(f\)
4) Tracer la courbe \(C\).
5) Soit la fonction \(F\) définie sur ]0,+∞[ par:
F(x)= \(\frac{x^{2}}{2}-x) ln x-\frac{x^{2}}{4}+x\)
a) Montrer que: \(F\) est une primitive de } \(f\) sur ]0,+∞[
b) Calculer l’aire de la partie du plan délimitée par la courbe \(C\),
l’axe des abscisses et les droites d’équations x=1 et x=e
* Suite Numérique (5 points )
Soit la suite réelle \((u_{n})\) définie sur IN par :
\(\{\begin{array}{l}u_{0}=0 \\ u_{n+1}=\frac{2}{1+u_{n}} \;pour\; tout\; n∈IN\; \end{array}.\)
1) a) Calculer \(u_{1}\) et \(u_{2}\) et en déduire que la suite \((u_{n})\) n’est pas monotone.
b) Montrer par récurrence que pour tout n∈IN : 0 ≤ u_{n} ≤ 2
2) Soit la suite \((v_{n})\) définie sur IN par:
\(v_{n}=\frac{u_{n}-1}{u_{n}+2}\) pour tout n∈IN
a) Montrer que :
la suite \((v_{n})\) est géométrique de raison \(-\frac{1}{2}\)
et déterminer \(\lim_{n➝+∞} v_{n}\)
b) Montrer que pour tout n∈IN : \(u_{n}=\frac{1+2 v_{n}}{1-v_{n}}\)
c) En déduire que la suite \((u_{n})\) est convergente.
⇊⇊Télécharger Fichier PDF Gratuit:
Bac Eco et Ges Ses Pri 2019
Bac Eco et Ges Ses Pri 2019
Correction
Bac Economie et Gestion Session Principale 2019 Pdf
* Calcule Matriciel
1) a) \(\operatorname{det}(A)=\left|\begin{array}{ccc}4 & -2 & 6 \\ 3 & -1 & 5 \\ -1 & 1 & -3\end{array}\right|\)
\[
\begin{array}{l}
=4\left|\begin{array}{cc}
-1 & 5 \\
1 & -3
\end{array}\right|-(-2)\left|\begin{array}{cc}
3 & 5 \\
-1 & -3
\end{array}\right|+6\left|\begin{array}{cc}
3 & -1 \\
-1 & 1
\end{array}\right| \\
& = 4 \times(-2)+2 \times(-4)+6 \times 2 \\
& = -4
\end{array}
\]
Comme \(\operatorname{det}(A) \neq 0,\) alors la matrice \(A\) est inversible.
\[
\begin{array}{l}
=4\left|\begin{array}{cc}
-1 & 5 \\
1 & -3
\end{array}\right|-(-2)\left|\begin{array}{cc}
3 & 5 \\
-1 & -3
\end{array}\right|+6\left|\begin{array}{cc}
3 & -1 \\
-1 & 1
\end{array}\right| \\
& = 4 \times(-2)+2 \times(-4)+6 \times 2 \\
& = -4
\end{array}
\]
Comme \(\operatorname{det}(A) \neq 0,\) alors la matrice \(A\) est inversible.
b) \(B-2 I_{3}=\left(\begin{array}{ccc}3 & 0 & 2 \\ -2 & 5 & 1 \\ -1 & 1 & 1\end{array}\right)-\left(\begin{array}{ccc}2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2\end{array}\right)\)
\(=\left(\begin{array}{ccc}1 & 0 & 2 \\ -2 & 3 & 1 \\ -1 & 1 & -1\end{array}\right)\)
\(A\left(B-2 I_{3}\right)=\left(\begin{array}{ccc}1 & -2 & 6 \\ 3 & -1 & 5 \\ -1 & 1 & -3\end{array}\right)\left(\begin{array}{ccc}1 & 0 & 2 \\ -2 & 3 & 1 \\ -1 & 1 & -1\end{array}\right)\)
\(=\left(\begin{array}{ccc}2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2\end{array}\right)=2 I_{3}\)
\(A\left(B-2 I_{3}\right)=2 I_{3} \Leftrightarrow A \times \frac{1}{2}\left(B-2 I_{3}\right)=I_{3}\)
Donc \(A^{-1}=\frac{1}{2}\left(B-2 I_{3}\right)=\left(\begin{array}{ccc}\frac{1}{2} & 0 & 1 \\ -1 & \frac{3}{2} & \frac{1}{2} \\ -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2}\end{array}\right)\)
2) a) \((\alpha, \alpha, 0)\) est une solution de \((S)\)
\[
\begin{array}{l}
\Leftrightarrow\left\{\begin{array}{l}
4 \alpha-2 \alpha=1 \\
3 \alpha-\alpha=2 \\
-\alpha+\alpha=1
\end{array}\right. \\
\Leftrightarrow\left\{\begin{array}{l}
\alpha=\frac{1}{2} \\
\alpha=1 \\
0=1
\end{array}\right.
\end{array}
\]
Donc il n’existe aucun réel \(\alpha\) pour lequel \((\alpha, \alpha, 0)\) soit une solution de \((S)\)
\[
\begin{array}{l}
\Leftrightarrow\left\{\begin{array}{l}
4 \alpha-2 \alpha=1 \\
3 \alpha-\alpha=2 \\
-\alpha+\alpha=1
\end{array}\right. \\
\Leftrightarrow\left\{\begin{array}{l}
\alpha=\frac{1}{2} \\
\alpha=1 \\
0=1
\end{array}\right.
\end{array}
\]
Donc il n’existe aucun réel \(\alpha\) pour lequel \((\alpha, \alpha, 0)\) soit une solution de \((S)\)
b) \((a, b, c)\) est une solution de \((S)\)
c) \((S) \Leftrightarrow\left(\begin{array}{l}x \\ y \\ z\end{array}\right)=\left(\begin{array}{ccc}\frac{1}{2} & 0 & 1 \\ -1 & \frac{3}{2} & \frac{1}{2} \\ -\frac{1}{2} & \frac{1}{2} & -\frac{1}{2}\end{array}\right) \times\left(\begin{array}{l}1 \\ 2 \\ 1\end{array}\right) \Leftrightarrow\left(\begin{array}{l}x \\ y \\ z\end{array}\right)=\left(\begin{array}{c}\frac{3}{2} \\ \frac{5}{2} \\ 0\end{array}\right)\)
\(S_{ R ^{3}}=\left\{\left(\frac{3}{2}, \frac{5}{2}, 0\right)\right\}\)
\(S_{ R ^{3}}=\left\{\left(\frac{3}{2}, \frac{5}{2}, 0\right)\right\}\)
* Statistique
1) a) Le nuage
b) Le nuage a une forme allongée, donc un ajustement affine est possible.
c) \(\bar{x}=5 ; \bar{y}=1500 ; G(5,1500)\)
2. a) Une équation de la droite \(D\) de régression de \(x\) en \(y\) est :
\(y=a x+b\)
Avec \(a=61\) et \(b=1195\)
Donc \(D: y=61 x+1195\)
\(y=a x+b\)
Avec \(a=61\) et \(b=1195\)
Donc \(D: y=61 x+1195\)
b) 2023 correspond à \(x=15\)
On estime le prix moyen d’un litre d’essence sans plomb en 2023 à:
\(y=61 \times 15+1195=2110\) dinars.
On estime le prix moyen d’un litre d’essence sans plomb en 2023 à:
\(y=61 \times 15+1195=2110\) dinars.
* Etude d’une fonction numérique
1) a) \(\lim _{x➝0^{+}} f(x)\)
\(=\lim _{x➝0^{+}}(x-1) \ln x\)
=+∞
car \(\lim _{x➝0^{+}} x-1=-1\)
et \(\lim _{x➝0^{+}} ln x=-∞\)
⇒La droite d’équation \(x=0\) est une asymptote verticale à la courbe \((C)\)
b) * \( \lim _{x➝+∞} f(x)\)
\(=\lim _{x➝+∞}(x-1) \ln x\)
=+∞
car \(\lim _{x➝+∞} x-1=+∞\)
et \(\lim _{x➝+∞} \ln x=+∞\)
* \(\lim _{x➝+∞} \frac{f(x)}{x}\)
\(=\lim _{x➝+∞} \frac{x-1}{x} \ln x \)
=+∞
car \(\lim _{x➝+∞} \frac{x-1}{x}=\lim _{x➝+∞} \frac{x}{x}=1\)
et \(\lim _{x➝+∞} \ln x=+∞\)
\(=\lim _{x➝0^{+}}(x-1) \ln x\)
=+∞
car \(\lim _{x➝0^{+}} x-1=-1\)
et \(\lim _{x➝0^{+}} ln x=-∞\)
⇒La droite d’équation \(x=0\) est une asymptote verticale à la courbe \((C)\)
b) * \( \lim _{x➝+∞} f(x)\)
\(=\lim _{x➝+∞}(x-1) \ln x\)
=+∞
car \(\lim _{x➝+∞} x-1=+∞\)
et \(\lim _{x➝+∞} \ln x=+∞\)
* \(\lim _{x➝+∞} \frac{f(x)}{x}\)
\(=\lim _{x➝+∞} \frac{x-1}{x} \ln x \)
=+∞
car \(\lim _{x➝+∞} \frac{x-1}{x}=\lim _{x➝+∞} \frac{x}{x}=1\)
et \(\lim _{x➝+∞} \ln x=+∞\)
\(\Rightarrow\) La courbe
\((C)\) admet une branche parabolique au voisinage de \(+\infty\) de direction celle de l’axe des
ordonnées.
2) \(\cdot \text { La fonction } x \longmapsto x-1 \text { est dérivable sur } R , \text { en particulier sur }] 0,+\infty[\)
・ La fonction \(x \longmapsto \ln x \text { est dérivable sur }] 0,+\infty[\)
Donc \(f \text { est dérivable sur }] 0,+\infty[\)
\[
f^{\prime}(x)=\ln x+(x-1) \frac{1}{x}=\ln x+\frac{x-1}{x}
\]
3) a)
b) Tableau de variation de \((f)\):
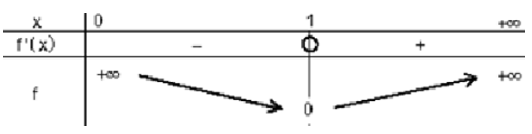
4)
5) a) \(F \text { est dérivable sur }] 0,+\infty[\)
\(
\begin{aligned}
F^{\prime}(x) &=\left(\frac{2 x}{2}-1\right) \ln x+\left(\frac{x^{2}}{2}-x\right) \frac{1}{x}-\frac{2 x}{4}+1 \\
&=(x-1) \ln x+\left(\frac{x^{2}}{2}-x\right) \frac{1}{x}-\frac{x}{2}+1 \\
&=(x-1) \ln x+\frac{x^{2}}{2} \frac{1}{x}-x \frac{1}{x}-\frac{x}{2}+1 \\
&=(x-1) \ln x+\frac{x}{2}-1-\frac{x}{2}+1=(x-1) \ln x=f(x)
\end{aligned}
\)
Donc \(F\) est une primitive de f sur] 0,+∞[
b) L’aire de la partie du plan limitée par la courbe \((C),\) l’axe des abscisses
b) L’aire de la partie du plan limitée par la courbe \((C),\) l’axe des abscisses
et les droites d’équations x=e et x=1 est:
\(\begin{aligned}
\qquad \begin{aligned}
A &=\int_{1}^{e}|f(x)| d x \\
&=\int_{1}^{e} f(x) d x \operatorname{car} f(x) \geq 0 \text { pour tout } x \in[1, e] \\
&=[F(x)]_{1}^{e} \\
&=F(e)-F(1) \\
&=\left(\frac{e^{2}}{2}-e\right) \ln e-\frac{e^{2}}{4}+e-\left(\left(\frac{1^{2}}{2}-1\right) \ln 1-\frac{1^{2}}{4}+1\right) \\
&=\frac{e^{2}}{2}-e-\frac{e^{2}}{4}+e-\left(-\frac{1}{4}+1\right) \\
&=\frac{e^{2}}{4}-\frac{3}{4} (u a)
\end{aligned}\end{aligned}\)
\(\begin{aligned}
\qquad \begin{aligned}
A &=\int_{1}^{e}|f(x)| d x \\
&=\int_{1}^{e} f(x) d x \operatorname{car} f(x) \geq 0 \text { pour tout } x \in[1, e] \\
&=[F(x)]_{1}^{e} \\
&=F(e)-F(1) \\
&=\left(\frac{e^{2}}{2}-e\right) \ln e-\frac{e^{2}}{4}+e-\left(\left(\frac{1^{2}}{2}-1\right) \ln 1-\frac{1^{2}}{4}+1\right) \\
&=\frac{e^{2}}{2}-e-\frac{e^{2}}{4}+e-\left(-\frac{1}{4}+1\right) \\
&=\frac{e^{2}}{4}-\frac{3}{4} (u a)
\end{aligned}\end{aligned}\)
* Suite Numérique
1) a) \(u_{1}=\frac{2}{1+u_{0}}=\frac{2}{1+0}=2\)
\(u_{2}=\frac{2}{1+u_{1}}=\frac{2}{1+2}=\frac{2}{3}\)
Comme \(u_{0}<u_{2}<u_{1},\)
\(u_{2}=\frac{2}{1+u_{1}}=\frac{2}{1+2}=\frac{2}{3}\)
Comme \(u_{0}<u_{2}<u_{1},\)
alors la suite \((u_{n})\) n’est pas monotone.
b) \(\ 0 ≤ u_{0}=0 ≤ 2\) vrai
Supposons que \(0 ≤ u_{n} ≤ 2\) et montres que \(0 ≤ u_{n+1} ≤ 2\)
\(\begin{aligned} 0 ≤ u_{n} ≤ 2 & ⇔ 1 ≤ 1+u_{n} ≤ 3 \\ & ⇔ \frac{1}{3} ≤ \frac{1}{1+u_{n}} ≤ 1 \\ & ⇔ \frac{2}{3} ≤ \frac{2}{1+u_{n}} ≤ 2 \\ & ⇔ \frac{2}{3} ≤ u_{n+1} ≤ 2 \end{aligned}\)
Donc \(0 ≤ \frac{2}{3} ≤ u_{n+1} ≤ 2\)
Conclusion : \(0 ≤ u_{n} ≤ 2\) pour tout \(n ∈IN\)
Supposons que \(0 ≤ u_{n} ≤ 2\) et montres que \(0 ≤ u_{n+1} ≤ 2\)
\(\begin{aligned} 0 ≤ u_{n} ≤ 2 & ⇔ 1 ≤ 1+u_{n} ≤ 3 \\ & ⇔ \frac{1}{3} ≤ \frac{1}{1+u_{n}} ≤ 1 \\ & ⇔ \frac{2}{3} ≤ \frac{2}{1+u_{n}} ≤ 2 \\ & ⇔ \frac{2}{3} ≤ u_{n+1} ≤ 2 \end{aligned}\)
Donc \(0 ≤ \frac{2}{3} ≤ u_{n+1} ≤ 2\)
Conclusion : \(0 ≤ u_{n} ≤ 2\) pour tout \(n ∈IN\)
2) a) \(v_{n}=\frac{u_{n}-1}{u_{n}+2}\)
\(v_{n+1}=\frac{u_{n+1}-1}{u_{n+1}+2}\)
\(=\frac{\frac{2}{1+u_{n}}-1}{\frac{2}{1+u_{n}}+2}\)
\(=\frac{\frac{2-1-u_{n}}{1+u_{n}}}{\frac{2+2+2 u_{n}}{1+u_{n}}}\)
\(=\frac{1-u_{n}}{4+4 u_{n}}\)
\(=-\frac{1}{2} \frac{u_{n}-1}{u_{n}+2}\)
\(=-\frac{1}{2} v_{n}\)
Donc \((v_{n})\) est une suite géométrique de raison \(q=-\frac{1}{2}\)
\((v_{n})\) est une suite géométrique de raison \(q=-\frac{1}{2} \in]-1,1[\)
\(v_{n+1}=\frac{u_{n+1}-1}{u_{n+1}+2}\)
\(=\frac{\frac{2}{1+u_{n}}-1}{\frac{2}{1+u_{n}}+2}\)
\(=\frac{\frac{2-1-u_{n}}{1+u_{n}}}{\frac{2+2+2 u_{n}}{1+u_{n}}}\)
\(=\frac{1-u_{n}}{4+4 u_{n}}\)
\(=-\frac{1}{2} \frac{u_{n}-1}{u_{n}+2}\)
\(=-\frac{1}{2} v_{n}\)
Donc \((v_{n})\) est une suite géométrique de raison \(q=-\frac{1}{2}\)
\((v_{n})\) est une suite géométrique de raison \(q=-\frac{1}{2} \in]-1,1[\)
alors \( \lim _{n➝+∞} v_{n}=0.\)
b)\(v_{n}=\frac{u_{n}-1}{u_{n}+2} ⇔ v_{n}(u_{n}+2)=u_{n}-1\)
\(⇔ v_{n} u_{n}+2 v_{n}=u_{n}-1\)
\(⇔ u_{n}-v_{n} u_{n}=1+2 v_{n}\)
\(⇔ u_{n}(1-v_{n})=1+2 v_{n}\)
\(\quad ⇔ u_{n}=\frac{1+2 v_{n}}{1-v_{n}}\)
\(⇔ v_{n} u_{n}+2 v_{n}=u_{n}-1\)
\(⇔ u_{n}-v_{n} u_{n}=1+2 v_{n}\)
\(⇔ u_{n}(1-v_{n})=1+2 v_{n}\)
\(\quad ⇔ u_{n}=\frac{1+2 v_{n}}{1-v_{n}}\)
c) \(\lim _{n➝+∞} u_{n}=\lim _{n➝+∞} \frac{1+2 v_{n}}{1-v_{n}}=1\)
(car \(\lim _{n➝+∞} v_{n}=0\))
Donc \((u_{n})\) converge vers 1
⇊⇊Télécharger Fichier PDF Gratuit:
Correction Bac Eco et Ges Princ 2019
➲ Si vous souhaitez signaler une erreur merci de nous envoyer un commentaire