Olympiade de Mathématiques
( compétition de mathématiques destinée aux élèves des lycées et collèges)
Olympiade Math – Géométrie 03 – Exercice 02
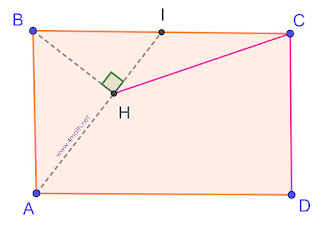
Soient ABCD un parallélogramme et I le milieu du segment [BC].
Soit H la projection orthogonale du point D sur La droite (AI).
Montrer que CH = CD.
Solution
Méthode 01 :
On prolonge la droite (AI)
On considère J le point d’intersection des droites (AI) et (CD).
On montre que le point C est le milieu de [DJ]
On montre que CH = CJ = CD
En considérant le triangle rectangle HDJ en H.
Méthode 02 :
On construit la parallèle a (AI) passant par C, elle coupe le segment [DH] en un point K.
On montre ensuite que la droite (CK) est la médiatrice de [DH] en utilisant la droite des milieux.
L’Olympiade Internationale de Mathématiques (OIM)


