Olympiade de Mathématique
( compétition de math destinée aux élèves des lycées et collèges)
Des exercices et sujets corrigés pour s’entraîner.
Olympiade de Math – Arithmétique Niveaux 02 – Exercice 10
Des exercices et sujets corrigés pour s’entraîner.
Olympiade de Math – Arithmétique Niveaux 02 – Exercice 10
Trouver le plus petit entier n ≥ 2
Tel que toutes les fractions suivantes: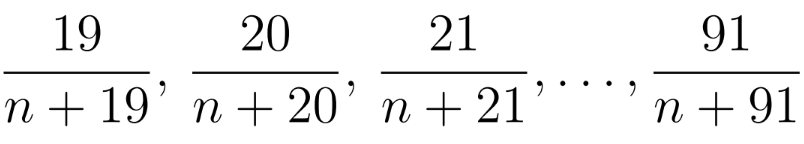
Tel que toutes les fractions suivantes:
soient irréductibles.
Solution:
Soit n∊IN.
* On a:
Solution:
Soit n∊IN.
* On a:
pour tout p = 19, 20,. . . , 91
d’après hypotypose:
➝ p/(n + p) est irréductible
➝ PGCD (p, (n + p))=1 ①
* d’autre part:
(n + p) − p = n
➝ PGCD (p, n + p) = PGCD (p, n)
①⤵️
PGCD (p, n) =1
* si n ∊{2, . . . , 18}
PGCD (p, n) ≠1
➝ n ∉ {2, . . . , 18}
* si n ∊ {19, . . . , 91}
PGCD (p, n) ≠1
➝ n ∉ {19, . . . , 91}
* si n ∊{2, . . . , 18}
PGCD (p, n) ≠1
➝ n ∉ {2, . . . , 18}
* si n ∊ {19, . . . , 91}
PGCD (p, n) ≠1
➝ n ∉ {19, . . . , 91}
* On déduire que n ≥ 92
et les facteurs premiers dans la décomposition de n doivent être supérieurs à 92 .
(en fait, sinon PGCD (p, n)≠1).
et les facteurs premiers dans la décomposition de n doivent être supérieurs à 92 .
(en fait, sinon PGCD (p, n)≠1).
On Conclure que le plus petit entier qui satisfait cette condition est 92.
Olympiade de Maths, c’est une gymnastique de l’esprit, Ce qu’il faut c’est 4 math .net et beaucoup de pratiques.
4 math .net Le première clé pour être bon en maths
4 math .net Le première clé pour être bon en maths