4 math Le première clé pour être bon en maths
Examen 08 Avec Solution
Mathématique Terminale S ( Bac 2 ) : Mars 2005
Mathématique Terminale S ( Bac 2 ) : Mars 2005
EXERCICE 1
On considère la fonction f , définie sur [1 ; +∞[ par :
1. a. Justifier la continuité de f sur [1 ; +∞[.
b. Montrer que f est croissante sur [1 ; +∞[.
2. Restitution organisée de connaissances
On pourra raisonner en s’appuyant sur le graphique fourni. Pour tout réel x0 de [1 ; +∞[, on note A (x0) l’aire du domaine délimité par la courbe représentant f dans un repère orthogonal, l’axe des abscisses et les droites d’équations x =1 et x = x0. On se propose de démontrer que la fonction ainsi définie sur [1 ; +∞[ est une primitive de f .
a. Que vaut A (1)?
b. Soit x0 un réel quelconque de [1 ; +∞[ et h un réel strictement positif.
Justifier l’encadrement suivant :
c. Lorsque x0 > 1, quel encadrement peut-on obtenir pour h < 0 et tel que x0 +h ⩾ 1?
d. En déduire la dérivabilité en x0 de la fonction A
ainsi que le nombre dérivé en x0 de la fonction A .
EXERCICE 2
Le plan complexe P est rapporté à un repère orthonormal direct.
On désigne par I le point d’affixe zI = 1, par A le point d’affixe zA = 1−2i, par B le point d’affixe −2+2i et par (C ) le cercle de diamètre [AB].
On fera une figure que l’on complètera avec les différents éléments intervenant dans l’exercice.
On prendra pour unité graphique 2 cm.
1. Déterminer le centre Ω du cercle (C) et calculer son rayon.
2. Soit D le point d’affixe zD =
Écrire zD sous forme algébrique puis démontrer que D est un point du cercle (C ).
3. Sur le cercle (C ), on considère le point E, d’affixe zE,
tel qu’une mesure en radians de
a. Préciser le module et un argument de zE+½.
b. En déduire que
4. Soit r l’application du plan P dans lui-même qui à tout point M d’affixe z associe le point M′ d’affixe z′tel que :
a. Déterminer la nature de r et ses éléments caractéristiques.
b. Soit K le point d’affixe zK = 2.
Déterminer par le calcul l’image de K par r . Comment peut-on retrouver
géométriquement ce résultat ?
EXERCICE 3
Le plan complexe est rapporté a un repère orthonormal direct
On considère l’application f qui au point M d’affixe z
fait correspondre le point M′ d’affixe z′ tel que :
1. On note x et x’, y et y’ les parties réelles et les parties imaginaires de z et z’.
Démontrer que :
2. a. Déterminer l’ensemble des points invariants par f .
b. Quelle est la nature de l’application f ?
3. Déterminer l’ensemble D des points M d’affixe z tels que z′ soit réel.
4. On cherche à déterminer les points de D dont les coordonnées sont entières.
a. Donner une solution particulière (x0 ; y0) appartenant à Z2 de l’équation: 4x −3y =2.
b. Déterminer l’ensemble des solutions appartenant à Z2 de l’équation: 4x −3y =2.
5. On considère les points M d’affixe z = x +iy tels que x = 1 et y ∈ Z.
Le point M′ = f (M) a pour affixe z′.
Déterminer les entiers y tels que Re(z′) et Im(z′) soient entiers
(on pourra utiliser les congruences modulo 5).
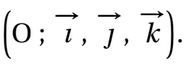

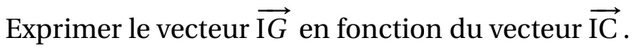
EXERCICE 5
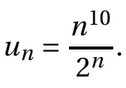

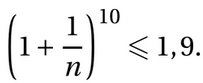
EXERCICE 4
L’espace E est rapporté à un repère orthonormal:
On considère les points A, B et C de coordonnées respectives
(1 ; 0 ; 2), (1 ; 1 ; 4) et (−1 ; 1 ; 1).
1. a. Montrer que les points A, B et C ne sont pas alignés.
En déduire une équation cartésienne du plan (ABC).
2. Soient P1 et P2 les plans d’équations respectives:
2x + y +2z +1 =0 et x −2y +6z =0.
a. Montrer que les plans P1 et P2 sont sécants
selon une droite D dont on déterminera un système d’équations paramétriques.
b. La droite D et le plan (ABC) sont-ils sécants ou bien parallèles ?
3. Soit t un réel positif quelconque.
On considère le barycentre G des points A, B et C affectés des coefficients respectifs 1, 2 et t.
a. Justifier l’existence du point G pour tout réel positif t.
Soit I le barycentre des points A et B affectés des coefficients respectifs 1 et 2. Déterminer les coordonnées du point I.
b. Montrer que l’ensemble des points G lorsque t décrit l’ensemble des nombres
réels positifs ou nuls est le segment [IC] privé du point C.
Pour quelle valeur de t, le milieu J du segment [IC] coïncide-t-il avec G ?
EXERCICE 5
Pour tout entier naturel n, on pose
On définit ainsi une suite (un) n∈N.
1. Prouver, pour tout entier naturel n non nul, l’équivalence suivante 
2. On considère la fonction f définie sur [1 ; +∞[ par:
a. Étudier le sens de variation et la limite en +∞ de la fonction f .
b. Montrer qu’il existe dans l’intervalle [1 ; +∞[ un unique nombre réel α tel
que f (α) =1,9. c. Déterminer l’entier naturel n0 tel que n0 −1 ⩽ α⩽ n0.
d. Montrer que, pour tout entier naturel n supérieur ou égal à 16, on a :
3. a. Déterminer le sens de variation de la suite (un) à partir du rang 16.
b. Que peut-on en déduire pour la suite ?
4. En utilisant un raisonnement par récurrence, prouver, pour tout entier natu-
rel n supérieur ou égal à 16, l’encadrement :
0 ⩽ un ⩽ 0,95n−16u16.
En déduire la limite de la suite (un )n∈N.
Examen Mathématique Terminale S ( Bac 2 )
4 math Le première clé pour être bon en maths

