Olympiade Math – Géométrie 02 – Ex 11

Olympiade de Mathématique 

( compétition de math destinée aux élèves des lycées et collèges)
Des exercices et sujets corrigés pour s’entraîner.

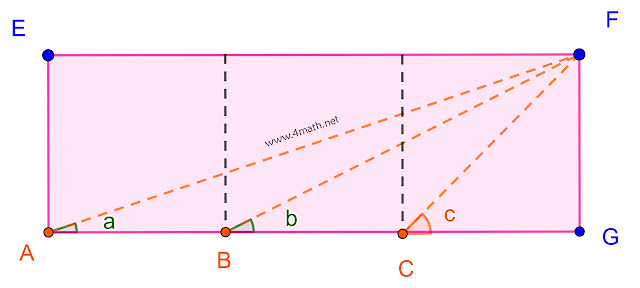
voir figure suivante:
(AEFG rectangle;AB=BC=CG)

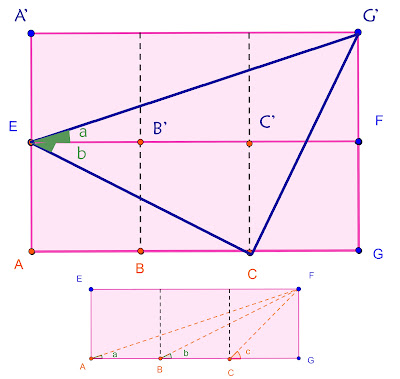
Montrer que a+b=c.
 On pose:
AB=a

* dans le Triangle CFG:
 On a GF=GC  
➝ c=45° ①

Soit la figure suivante

 * les Triangle AFG & EFG’ sont semblables:
 (FG=G’F=a & AG=EF=3a & angle droit )
➝ FE᳐G’=a
 * de même pour les Triangle ECC’ & BGF
➝ CȆF=b

* d’autre part:

les Triangle CGG’ & EAC sont semblables:
 (CG=EA=a & GG’=AC=3a & angle droit )
➝ CE᳐F+EC᳐A=90°
➝ G’C᳐E=90° & CG’=CE
➝ le triangle CG’E est rectangle isocèle en C:
 ➝a+b=45° ②
①&②
➨a+b=c  

Liens utiles :
L’Olympiade Internationale de Mathématiques (OIM)
site officiel de l’OIM, fondation de l’OIM

Olympiade de Maths, c’est une gymnastique de l’esprit, Ce qu’il faut c’est 4math.net et beaucoup de pratiques. 4math.net Le première clé pour être bon en maths