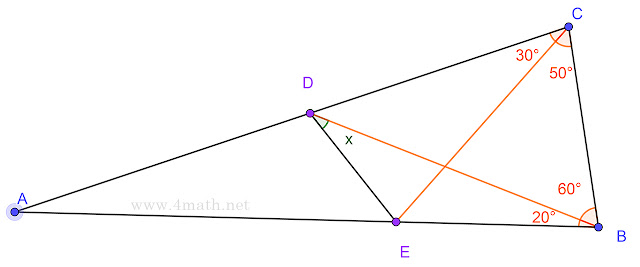
Soit la figure suivante:
Solution
On introduit les points F ,G et H
Tel que BĈF=60°
(voir figure suivante) :
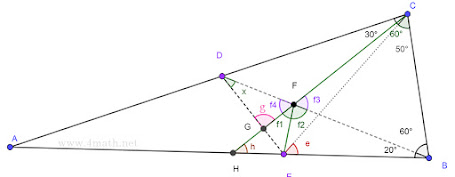
* dans le triangle BCE
e+50°+60°+20°=180°
➝ e=50°
➝ BEC est isocèle en B
➝ BC=BE ①
* dans le triangle BCF
➝ f₃+60°+60°=180°
➝ f₃=60° (a)
➝ BF=CF=BC ②
①&②
➝ BF=CF=BC=BE ③
* dans le triangle BEF
➝ BE=BF
➝ BEF est isocèle en B
➝ BÊF=f₂
Somme des angle de BEF
➝ BÊF+f₂+20°=180°
➝ 2 f₂= 160°
➝ f₂=80° (b)* Angle plat CF̂H
➝ f₁+f₂+f₃=180°
* (a)&(b)
➝ f₁+80°+60°=180°
➝ f₁=40° ④
* dans le triangle CHB
➝ 60°+h+20°+60°=180°
➝ h=40° ⑤
* ④&⑤➝ f₁=h
➝ EF=EH Ⓒ
* dans les triangle CBH & DCB
on a
* CB̂H=DĈB=80°
* HĈB=CB̂D=60°
( deux triangles ont même côté BC compris entre deux angles de même mesure alors ils sont égaux)
➝ CBH & DCB sont égaux
➝ BD=CH
* ③➝ BF=CF
➝ BD-BF=CH-CF
➝ DF=HF & f₄=60°
➝ DFH est équilatéral.
➝ DF=DH Ⓓ* Ⓒ&Ⓓ
➝ EF=EH & DF=DH
Donc (ED) est la médiatrice de [FG]
➝ g=90°* dans le triangle FDG
➝ x+f₄+g=180°
➝ x+60°+90°=180°

➡️ x=30°