Olympiade de Mathématique
( compétition de math destinée aux élèves des lycées et collèges)
Des exercices et sujets corrigés pour s’entraîner.
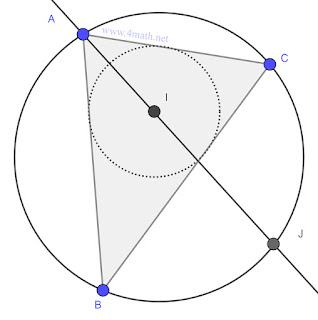
Soit ABC un triangle,
I le centre de son cercle inscrit.
La droite (AI) recoupe le cercle circonscrit à ABC en un point J.
Montrer que
JB = JC = JI.
Solution:
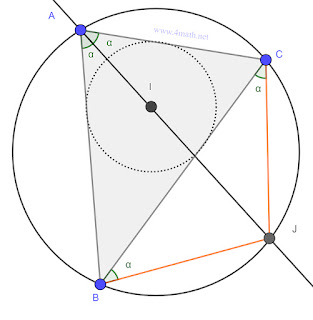
On utilisant théorème d’angles inscrits
On a
* (A, B, J et C étant cocycliques)
➝ BÂJ = BĈJ & CÂJ = CB̂J. ⓐ
* (AI) est bissectrice de BAC,
➝CÂJ= BÂJ ⓑ
ⓐ &ⓑ BĈJ = CB̂J
➝Triangle BCJ isocèle ▶️ JB = JC (1)
D’autre part
* Dans le Triangle AIB
➝ a+b+c=180° ①
* Les trois points A, I, J sont alignés
c+d=180° ②
①-② d=a+b ③
* (BI) est bissectrice de ABC
➝ b=g
* Théorème d’angles inscrits
➝ a=e
③ ➝ d=e+g
donc IJB est un triangle isocèle,
▶️ IJ=BI (2)
(1)&(2) ▶️ JB = JC = JI.
Liens utiles :
Olympiade de Maths, c’est une gymnastique de l’esprit, Ce qu’il faut c’est 4math.net et beaucoup de pratiques
4math.net Le première clé pour être bon en maths