Projection en ⑥ étapes
1- Projection sur une droite:
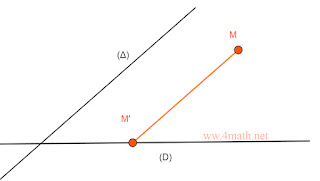
Soient (D) et (Δ) deux droites sécantes du plan (P).
Soit M∈P.
La droite parallèle à (Δ) issue de M
▶️ p (M) = M’
coupe la droite (D) en un point M’.
Le point M’ est appelé projeté du point M sur (D) parallèlement à la droite (Δ) on note :
▶️ p (M) = M’
p est appelée projection sur (D) parallèlement à (Δ).
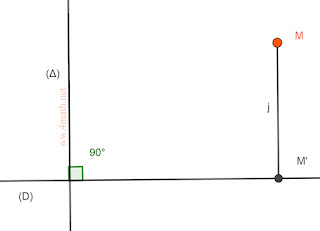
2- projection orthogonale:
Si (D) et (Δ) sont perpendiculaires du plan (P).
Le point M’, projeté de M sur (D) parallèlement à (Δ),
est appelé projeté orthogonal du point M sur la droite (D)
est appelé projeté orthogonal du point M sur la droite (D)
on note :
▶️ p (M) = M’
3- Théorème de Thalès:
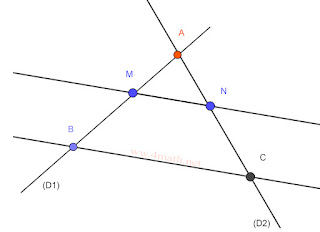
Soient (D₁) et (D₂) deux droites sécantes en un point A.
Soient B∈(D₁) et M∈(D₁) tel que B≠ A et M≠ A.
Soient C∈(D₂) et N∈(D₂) tel que B≠ A et M≠ A.
Si (MN) // (BC).
Soient (D₁) et (D₂) deux droites sécantes en un point A.
Soient B∈(D₁) et M∈(D₁) tel que B≠ A et M≠ A.
Soient C∈(D₂) et N∈(D₂) tel que B≠ A et M≠ A.
Si (MN) // (BC).
alors ▶️
AM AN MN
––––– = ––––– = –––––
AB AC BC
4- Réciproque du Théorème de Thalès:
Soient (D₁) et (D₂) deux droites sécantes en un point A.
Soient B∈(D₁) et M∈(D₁) tel que B≠ A et M≠ A.
Soient C∈(D₂) et N∈(D₂) tel que B≠ A et M≠ A.
Soient (D₁) et (D₂) deux droites sécantes en un point A.
Soient B∈(D₁) et M∈(D₁) tel que B≠ A et M≠ A.
Soient C∈(D₂) et N∈(D₂) tel que B≠ A et M≠ A.
si ona:
AM AN
––––– = –––––
AB AC
et si les points A, B, M et les points A, C, N sont dans
le même ordre.
alors ▶️ (MN) // (BC).
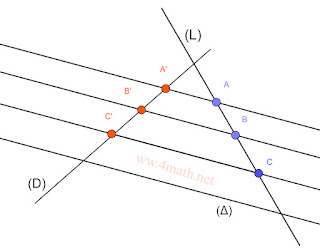
5- Théorème de Thalès par la projection:
Soient (D) et (L) deux droites.
Soit (Δ) une droite non parallèle à (D) et non parallèle à (L).
Soient A, B, C des points de (L) tels que A et B soient distincts.
si A’,B’,C’ sont les projetés respectifs de A,B,C sur (D) parallèlement à (Δ)
alors ▶️
AB A’B’
––––– = –––––
AC A’C’
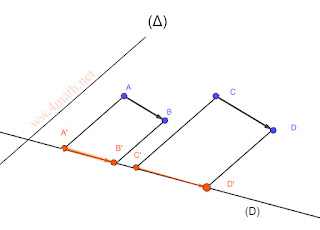
6- Conservation du coefficient de colinéarité de deux vecteurs:
Soient (D) et (Δ) deux droites sécantes.
–→ →
AB et CD deux vecteurs colinéaires tel que:
→ →
CD=k AB
si A’, B’, C’, D’ sont les projetés respectifs des points A, B, C, E
sur (D) parallèlement à la droite (Δ),
alors ▶️
alors ▶️
→ →
C’D’=k A’B’.
______________________________________________________________
Cours math Tronc Commun –––––––––– ⇲ Projection en ⑥ étapes