Olympiade Math – Géométrie 01 – Ex 10

Olympiade de Mathématiques
( compétition de math destinée aux élèves des lycées et collèges)


▶️Olympiade Math – Géométrie 01 – Exercice 10
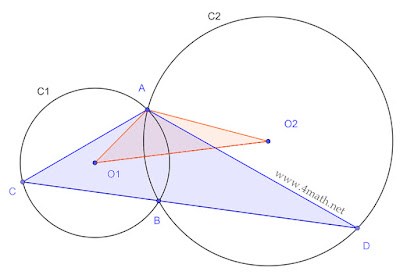
(C₁) et (C₂) deux cercles de centres respectifs O₁ et O₂ s’intersectant en A et B .
Soit C un point de (C₁) et D l’intersection de CB et (C₂). 
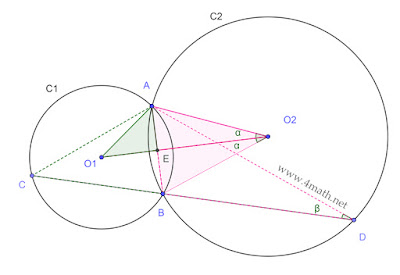
Montrer que AO₁O₂ et ACD sont semblables.

Solution 

Soit E l’intersection de (O₁O₂) et (AB)
On a
AO₁=AO₂ & BO₁=BO₂
AE=EB car (O₁O₂) médiatrice de [AB])
AO₁O₂ & BO₁O₂ sont semblables
AÔ₂E=EÔ₂B=α (voir figure)
On effectue une chasse aux angles : 
en posant AÔ₂B = 2α.
on trouve AD̂B = AÔ₂B/2=β=α.
AD̂B =AÔ₂E ①
* de même pour
BĈA=EÔ₁A ②
①&②
▶️ AO₁O₂ et ACD sont semblables.

Liens utiles : 
L’Olympiade Internationale de Mathématiques (OIM)
site officiel de l’OIM, fondation de l’OIM

Olympiade de Maths, c’est une gymnastique de l’esprit, Ce qu’il faut c’est 4math.net et beaucoup de pratiques

4math.net Le première clé pour être bon en maths