Olympiade de Mathématique
( compétition de math destinée aux élèves des lycées et collèges)
Des exercices et sujets corrigés pour s’entraîner.
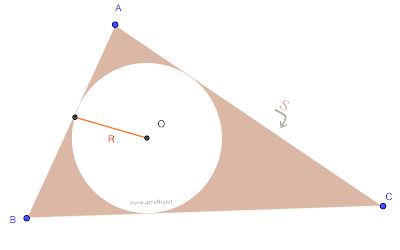
Soit ABC un triangle tel que: AB=13cm, AC=14cm, BC=15cm,
O le centre du cercle inscrit au triangle ABC et R son rayon.
Calculer la surface S
Solution:
∸∸∸
1-ⅠⅠ Calcul de la surface d’un triangle ABC en fonction de R
ona SABC = SAOB + SAOC + SBOC
⊸ SAOB ＝ AB྾R /2 ＝ 13R / 2
⊸ SAOC ＝ AC྾R /2 ＝14 R /2
⊸ SBOC ＝ BC྾R /2 ＝ 15 R /2
⇾ SABC =13྾R /2 + 14྾R /2 + 15྾R/2
▶️ SABC= 21྾R ①
∸∸∸
∸∸∸
2-ⅠⅠ Calcul de R
Calculon la surface de ABC d’autre maniéré
SABC = AD྾BC /2
théorème de Pythagore
⊸ Sur ABD
⇾ AC²=CD²+AD² ⓐ
⊸ Sur ACD
⇾ AB²=BD²+AD² ⓑ
ⓐ-ⓑ AC²-AB²=CD²-BD²=(CD+BD)྾(CD-BD) = BC྾(CD-BD)
⇾ 14²-13²=15྾(CD-BD)
⇾ CD-BD=1,8 & CD+BD=BC=15 ▶️ BD= (15-1,8)/2 = 6,6
⊸ AB²=BD²+AD² ⇾ 12²=6,6²+AD² ▶️ AD= 11,2
▶️ SABC = AD྾BC /2=11,2྾15 / 2 = 84
① ⇾ 21྾R=84 ▶️ R=4 cm
∸∸∸
3-ⅠⅠ Calcul de la surface S
⊸ S ＝ SABC – S(c) ፤ S(c) ＝ π྾R²＝ 3,14 R²
▶️ S = ( 21྾R -3,14྾R² ) = 33,76 cm
pour les élevés qui aiment
« comprendre », « résoudre » et découvrir de nouvelles façons de raisonner